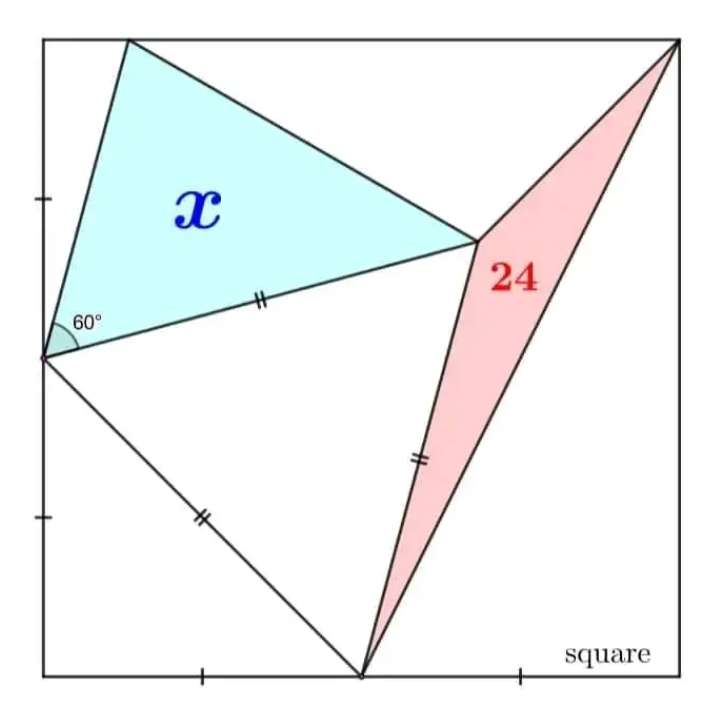
Mathematics Question and Solution
Calculating area x.
Let the square side length be 2a.
b² = a²+(2a)²
b = √(5a²)
b = √(5)a units.
c² = 2a²
c = √(2)a units.
c is the side length of the inscribed regular triangle (equilateral triangle).
tand = 2a/a
d = atan(2)°
It implies;
45+60+e+atan(2) = 180
e = (75-atan(2))°
e = 11.5650511771°
Therefore;
0.5*√(5)a*√(2)a*sin11.5650511771 = 24
√(5)a*√(2)a*sin11.5650511771 = 48
a² = 48/(√(10)sin11.5650511771)
a² = 75.7128129211
a = √(75.712812921)
a = 8.7013109886 units.
2a = 2*8.7013109886
= 17.4026219773 units.
Where 17.4026219773 units is the side length of the square.
c = √(2)a
And a = 8.7013109886 units.
c = √(2)*8.7013109886
c = 12.3055120106 units.
Again, c is the side length of the equilateral triangle.
f = 180-60-60-45
f = 15°
cos15 = 8.7013109886/g
g = 9.0082600048 units.
Therefore, area x is;
0.5*9.0082600048*12.3055120106sin60
= 48 square units.