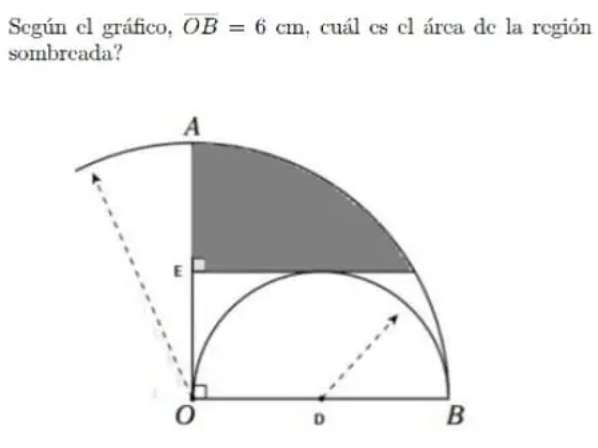
Notice.
OE = AE = ½(6)
OE = AE = 3 cm.
a²+3² = 6²
a² = 36-9
a = √(27)
a = 3√(3) cm.
tanb = a/3
b = atan(√(3))
a = 60°
Shaded Area is;
(0.5*3*3√(3))+(60π*6*6/360)-(0.5*6*6sin60...
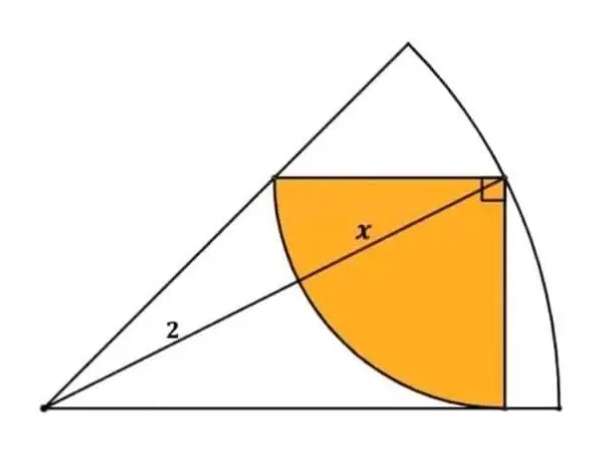
a = (2+x) units.
a is the radius of the ascribed sector.
b = 2x units.
x is the radius of the inscribed quarter circle.
Calculating x.
(2+x)² = x²+(2x)²
4+4x+x² = 5x²
x²-x-1 = 0
(x-½)...

Calculating x.
2*2^(x)-9^(x) = 0
2*2^(x) = 9^(x)
Dividing through by 2^(x).
2 = (4.5)^(x)
Taking log base 10 at both sides of the equation.
log2 = log(4.5)^(x)
x = log2/log(4.5)
x =...
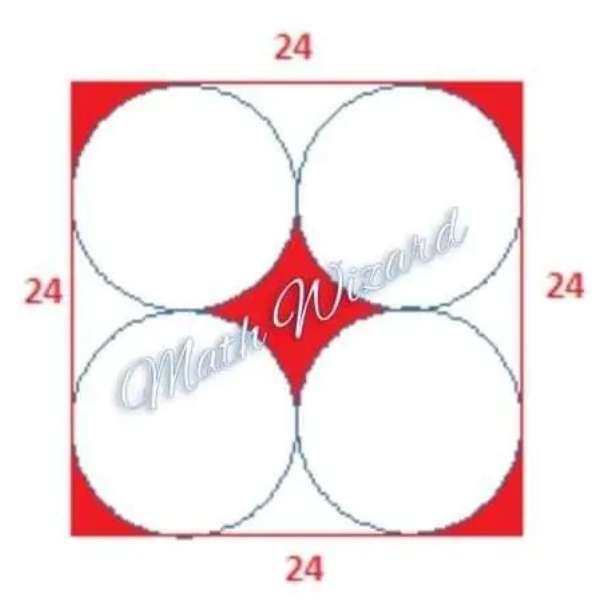
Area red is;
½(area square with single side length 24 units - 4(area circle with radius 6 units))
= ½(24²-4(36π))
= ½(576-144π)
= 288-72π
= 72(4-π) square units.
Or
2(area square wit...
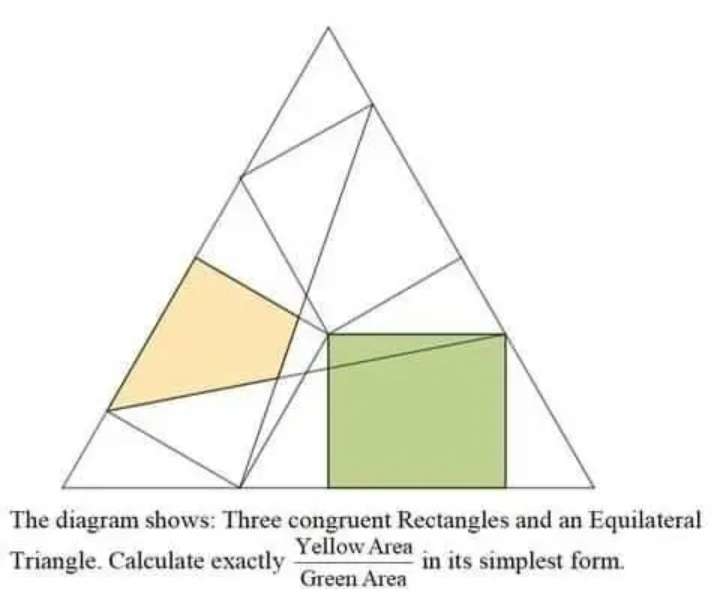
Sir Mike Ambrose is the author of the question.
Let the single side length of the equilateral triangle be 2 unit.
Therefore;
Area Green is;
⅓√(3) * ⅔
= 2√(3)/9 square units.
Area Yellow...
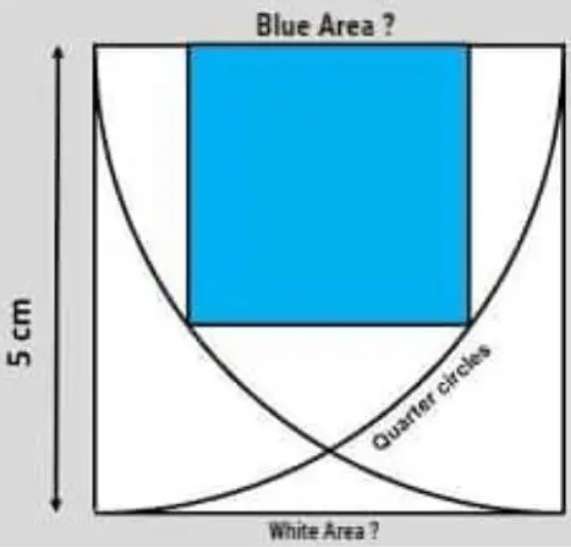
Let the single side length of the blue area/square be x.
Therefore;
5² = x² + (x+½(5-x))²
5² = x² + (½(5+x))²
25 = x² + ¼(25+10x+x²)
100 = 4x²+25+10x+x²
5x²+10x-75=0
x²+2x-15=0
(x+1)²=1...
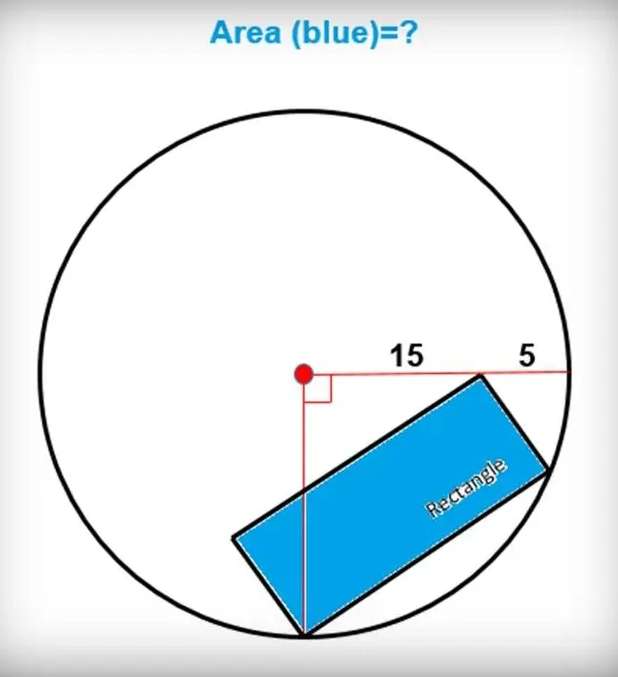
a = 15+5
a = 20 units.
a is the radius of the circle.
d² = b²+c² --- (1).
Where b is the width of the inscribed blue rectangle area and c is the length.
15²+20² = d²
d = 25 units.
d is t...
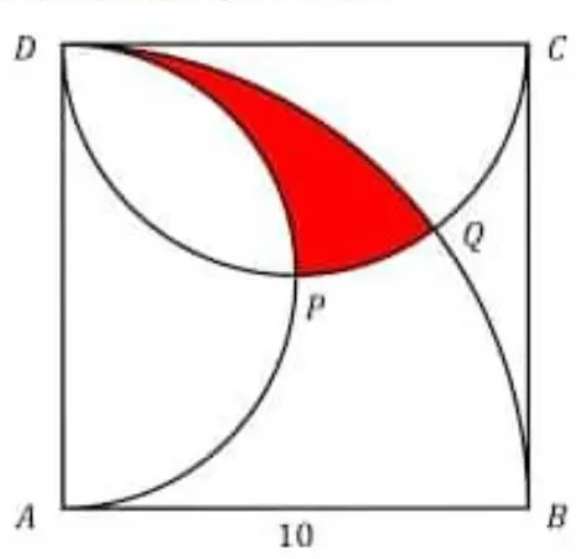
Area red is;
Area semi circle with radius 5 cm - Area sector with radius 5 cm and angle (180-2atan(2))° - Area kite with diagonal lengths √(10²+5²) cm and √(200-200cos(2atan(½))) cm + Area secto...
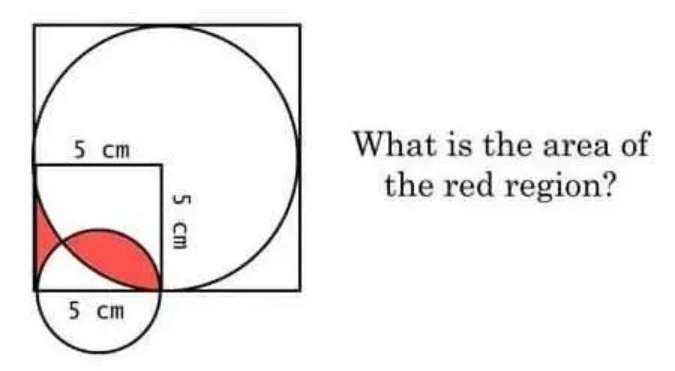
Area red is;
Area square with length 5 cm - Area quarter circle with radius 5 cm - Area sector with radius 2.5 cm and angle (180-2atan(2))° - Area kite with diagonal lengths √(5²+(2.5)²) cm and...
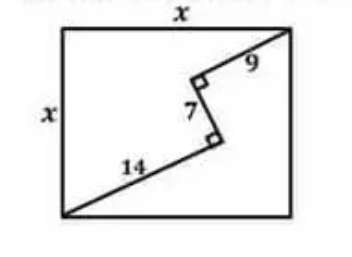
Calculating z, the diagonal of the square.
9 - 14
y - 7
Cross Multiply.
Therefore;
14y = 63-9y
23y = 63
y = 63/23 units.
z = √(9²+y²)+√(14²+(7-y)²)
And y = 63/23 units.
z...