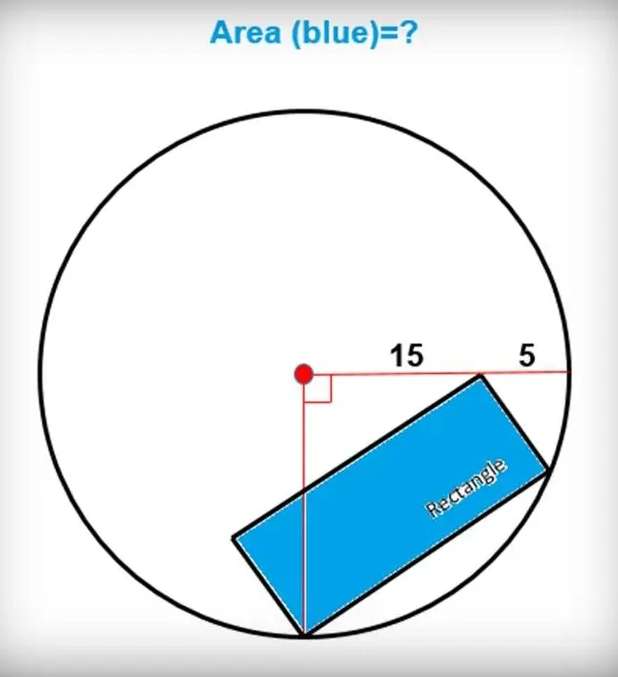
Mathematics Question and Solution
a = 15+5
a = 20 units.
a is the radius of the circle.
d² = b²+c² --- (1).
Where b is the width of the inscribed blue rectangle area and c is the length.
15²+20² = d²
d = 25 units.
d is the diagonal of the inscribed blue rectangle.
Substituting d is (1) making c the subject formula.
d² = b²+c²
25² = b²+c²
c = √(625-b²) units.
e = d+b
e = (25+b) units.
f = 2a
f = 40 units.
Calculating b.
40² = √(625-b²)²+(25+b)²
1600 = 625-b²+625+50b+b²
1600 = 1250+50b
160 = 125+5b
5b = 35
b = 7 units.
Again, b is the width of the inscribed blue rectangle.
Recall.
c = √(625-b²)
And b = 7 units.
c = √(625-49)
c = √(576)
c = 24 units.
Again, c is the length of the inscribed blue rectangle.
Area inscribed blue rectangle is;
bc
= 7*24
= 168 square units.