Mathematics Question and Solution
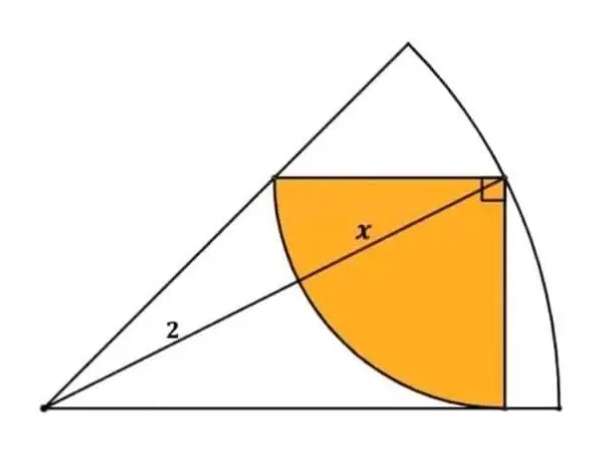
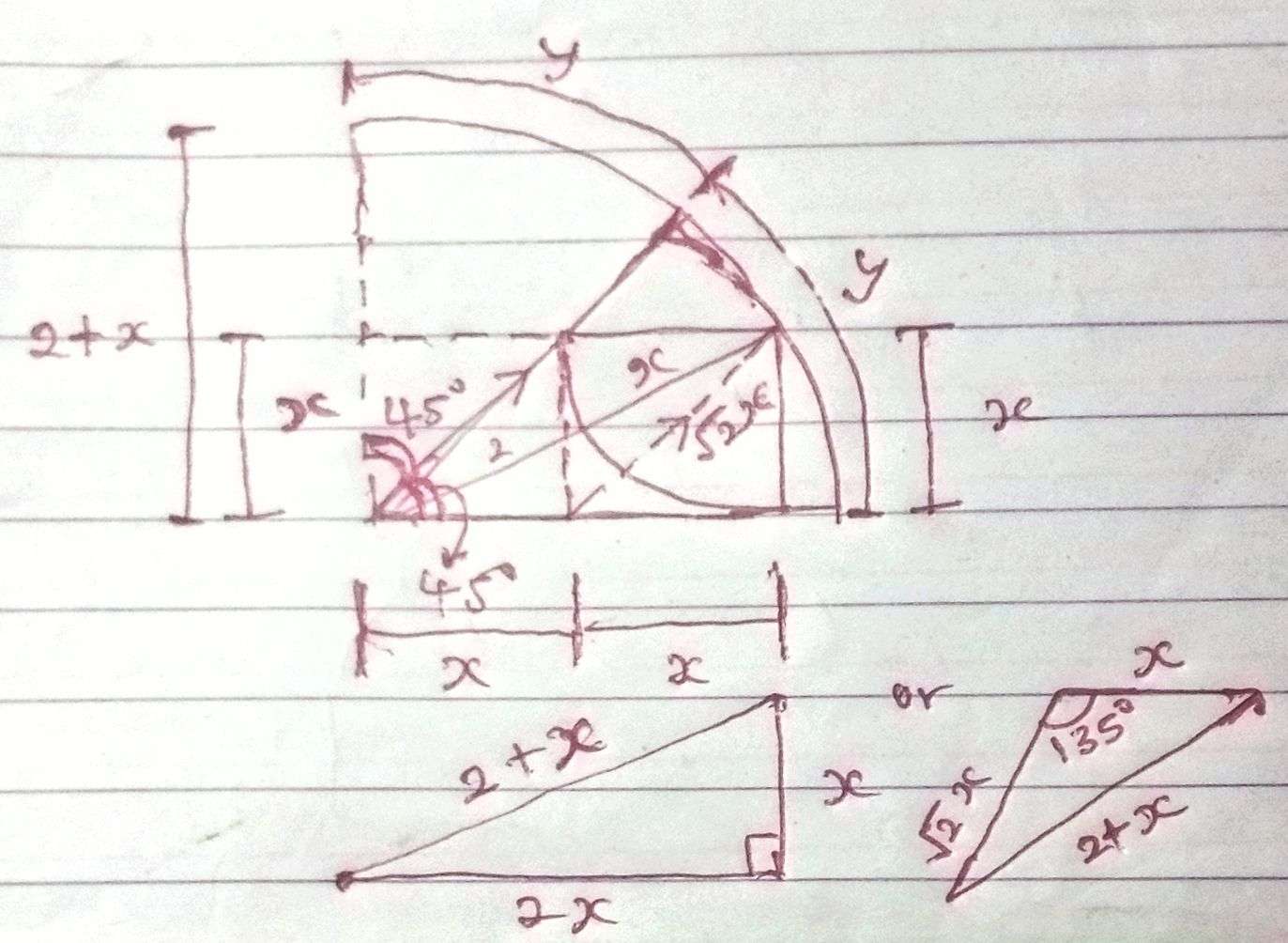
a = (2+x) units.
a is the radius of the ascribed sector.
b = 2x units.
x is the radius of the inscribed quarter circle.
Calculating x.
(2+x)² = x²+(2x)²
4+4x+x² = 5x²
x²-x-1 = 0
(x-½)² = 1+(-½)²
(x-½)² = (5/4)
x = ½±√(5/4)
x = ½±½√(5)
It implies;
x = ½(1+√(5)) units.
x = 1.6180339887 units.
Therefore, area inscribed quarter circle is;
¼(x²)π
= ¼*½(1+√(5))*½(1+√(5))π
= π(1+√(5))²/16
= 2.0561990865 square units.