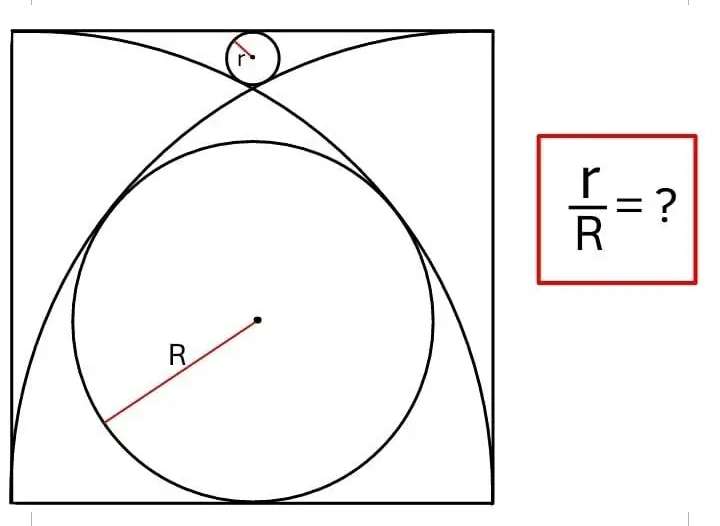
Mathematics Question and Solution
Let R be 1 unit (radius of the inscribed big circle).
Let a be the ascribed square side length.
Calculating a.
(a-1)² = 1²+(0.5a)²
a²-2a+1 = 1+¼(a²)
4a²-a² = 8a
3a = 8
a = ⅓(8) units.
Again, a is the side length of the ascribed square.
sin60 = b/a
½√(3) = b/(⅓(8))
⅓(8√(3)) = 2b
b = ⅙(8√(3)) units.
b = ⅓(4√(3)) units.
c = a-r
c = (⅓(8)-r) units.
d = (⅓(8)+r) units.
Calculating r, radius of the small inscribed circle.
d² = c²+r²
(⅓(8)+r)² = (⅓(8)-r)²+(½*⅓(8))²
⅑(64)+⅓(16r)+r² = ⅑(64)-⅓(16r)+r²+⅑(16)
⅔(16r) = ⅑(16)
(⅔)r = ⅑
2r = ⅓
r = ⅙ units.
It implies;
r/R is;
= ⅙÷1
= ⅙