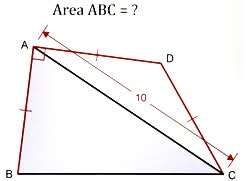
Mathematics Question and Solution
Let a = AB = AD = CD.
b² = 2a²
b = √(2)a units.
b is BD.
Notice.
Triangle BCD is a right-angled triangle, where BC is the hypotenuse.
c² =(√(2)a)²+a²
c = 3a²
c = √(3)a units.
c is BC.
cosd = (0.5*10)/a
cosd = 5/a --- (1).
d is angle CAD.
From (1).
sind = √(a²-25)/a --- (2).
(√(3)a)² = a²+10²-2a*10cos(90-d)
3a² = a²+100-20a(cos90cosd+sin90sind)
2a² = 100-20a(sind)
a² = 50-10asind --- (3).
Calculating a.
Substituting (2) in (3).
a² = 50-10a√(a²-25)/a
a² = 50-10√(a²-25)
10²(a²-25) = (50-a²)²
100a²-2500 = 2500-100a²+a⁴
a⁴-200a²+5000 = 0
(a²-100)² = -5000+(100)²
(a²-100)² = 5000
a² = 100±√(5000)
a² = 100±50√(2)
Therefore;
a ≠√(100+50√(2))
a = √(100-50√(2)) units.
a = 5.41196100146 units.
Recall.
cosd = 5/a --- (1).
And a = 5.41196100146 units.
cosd = 5/5.41196100146
d = 22.5°
e = 90-d
e = 90-22.5
e = 67.5°
e is angle BAC.
Therefore, Area Triangle ABC is;
½*5.41196100146*10sin(67.5)
= 25 square units.