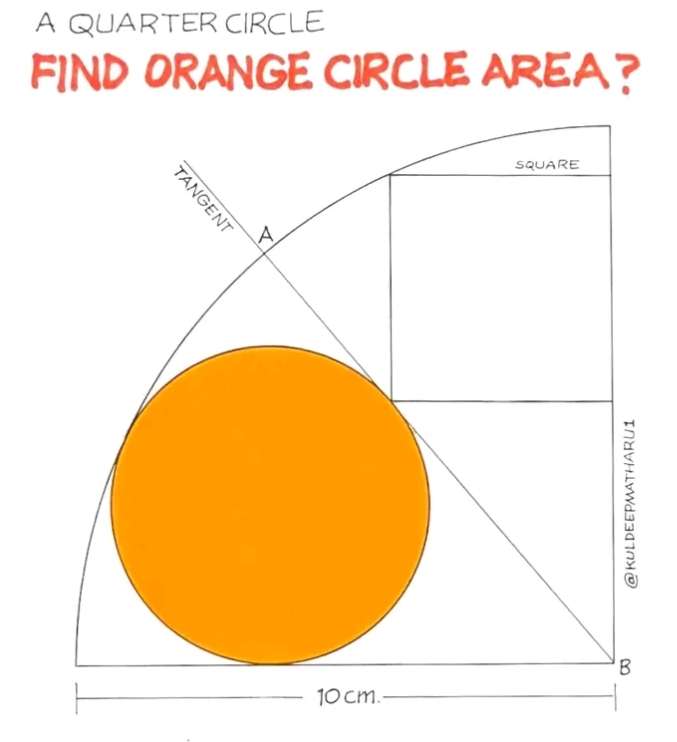
Mathematics Question and Solution
Let the inscribed square side be a.
b² = 2a²
b = √(2)a cm.
b is the diagonal of the inscribed square.
c = 90+45
c = 135°
It implies, calculating a, the inscribed square side length.
10² = 5²+(√(2)a)²-2*5*√(2)acos135
100 = 25+2a²+10a
2a²+10a-75 = 0
Resolving the above quadratic equation via completing the square approach to get a, the side length of the inscribed square.
(a+(5/2))² = (75/2)+(5/2)²
(a+(5/2))² = ¼(150+25)
(a+(5/2))² = ¼(175)
a = -(5/2)±√(¼(175))
a = -(5/2)±(5√(7)/2)
It implies;
a = ½(5√(7)-5) cm.
a = 4.1143782777 cm.
Again, a is the side length of the inscribed square.
d² = 5²+4.1143782777²
d = 6.4751917818 cm.
e = (10-r) cm.
r is the radius of the inscribed orange circle.
It implies;
(10-r)² = r²+6.4751917818²
100-20r+r² = r²+41.9281086111
20r = 100-41.9281086111
20r = 58.0718913889
r = 2.9035945694 cm.
It implies, area inscribed orange circle is;
πr²
= π(2.9035945694)²
= 26.4863323122 cm²