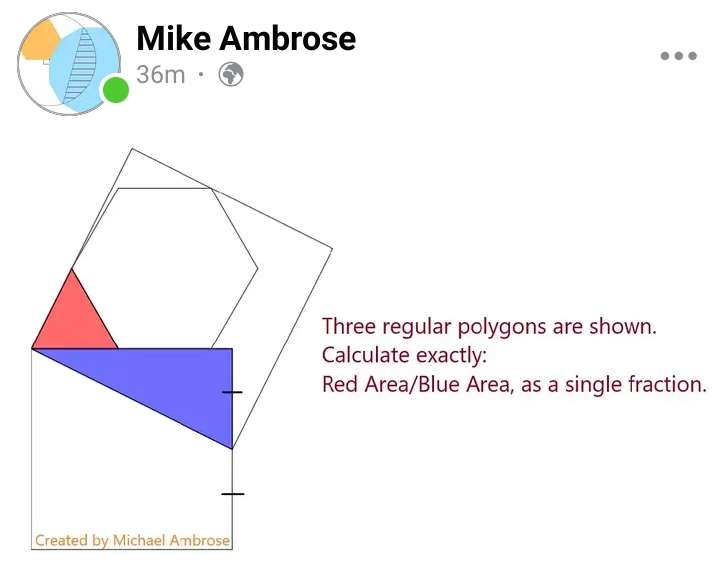
Mathematics Question and Solution
Let the small square side be 2 units.
Area Blue is;
0.5*2*1 = 1 square unit.
a² = 2²+1
a = √(5) units.
a is the side of the big square.
b = (90-atan(½))°
c = 180-(90-atan(½))-60
c = (30+atan(½))°
d = 180-90-(30+atan(½))
d = (60-atan(½))°
Let the side length of the inscribed regular hexagon be e.
(e/sin(90-atan(½))) = (f/ sin60)
f = 0.96824583655e units.
g = (√(5)-0.96824583655e) units.
cos(60-atan(½)) = (√(5)-0.96824583655e)/h
h = (2.67949192431-1.16025403784e) units.
j = 2(e/2)+e
j = 2e units.
It implies;
e²+(2.67949192431-1.16025403784e)² = (2e)²
e²+7.17967697244-6.21778264908e+1.34618943232e² = 4e²
1.65381056768e²+6.21778264908e-7.17967697244 = 0
Resolving the quadratic equation to get e.
e = 0.926421 units.
e is the side length of the inscribed regular hexagon.
Recall;
f = 0.96824583655e, and e is 0.926421 units.
f = 0.926421*0.96824583655
f = 0.89700327614 units.
Therefore;
Area Red is;
0.5*0.89700327614*0.926421sin(30+atan(½))
= 0.34674082191 square units.
Area Red ÷ Area Blue exactly in decimal is;
0.34674082191÷1
= 0.34674082191
≈ 0.35 to 2 decimal places.