Mathematics Question and Solution
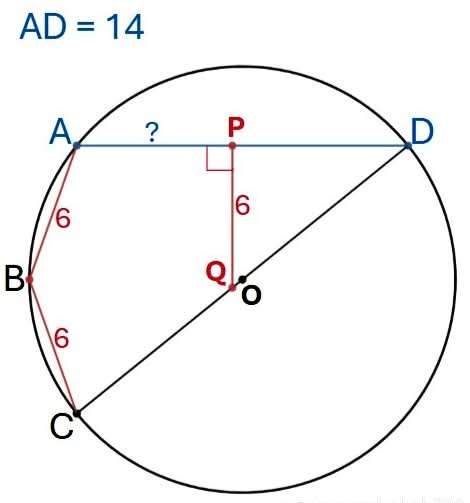
Let a be the diameter of the circle.
x² = 6²+6²+2*6*6cosb
x² = 72+72cosb --- (1).
x² = 14²+a²-2*14acosb
x² = 196+a²-28acosb --- (2).
Notice.
x is length AC
b is angle ADC.
cosb = 14/a --- (3).
Calculating a.
Equating (1) and (2).
72+72cosb = 196+a²-28acosb --- (4).
Substituting (3) in (4).
72+72(14/a) = 196+a²-28a(14/a)
72+72(14/a) = 196+a²-28(14)
72a+1008 = 196a+a³-392a
a³-268a-1008 = 0
Therefore;
a = 18 units.
Again, a is the diameter of the circle.
Recall.
cosb = 14/a --- (3).
And a = 18 units.
cosb = 14/18
b = acos(7/9)°
b = 38.942441269°
b is angle ADC.
It implies;
tan38.942441269 = 6/c
c = 6/tan38.942441269
c = 7.42462120246 units.
c is DP.
Therefore, the required length, AP is;
AD-DP
AP = 14-7.42462120246
AP = 6.57537879754 units.