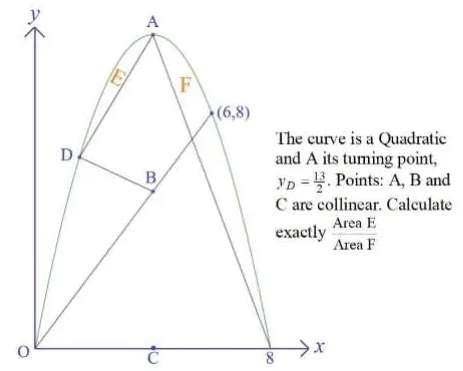
Mathematics Question and Solution
Equation of the curve is;
y = ⅔(8x-x²)
Calculating Area E.
(Area under the curve at x = (3/2) and x = 4) - Area trapezium with parallel sides (13/2) units and (10⅔) units, and height (5/3) units.
=(835/36) - ½*(5/2)*((13/2)+(32/3))
= (835/36) - (515/24)
= (125/72) square units.
Calculating Area F.
½(Area under the curve at x = 0 and x = 8) - Area triangle with height (32/3) units and base 4 units - Area triangle with height 6 units and base 8 units - (Area under the curve at x = 6 and x = 8) + Area triangle with height (64/9) units and base 8 units.
= (256/9) - ½*4*(32/3) - ½*6*8 - (80/9) + ½*8*(64/9)
= (256/9) - (64/3) - 24 - (80/9) + (256/9)
= (512/9) - (80/9) - (64/3) - 24
= (80/3) - 24
= (8/3) square units.
It implies;
Area E ÷ Area F exactly is;
(125/72) ÷ (8/3)
= 125/192