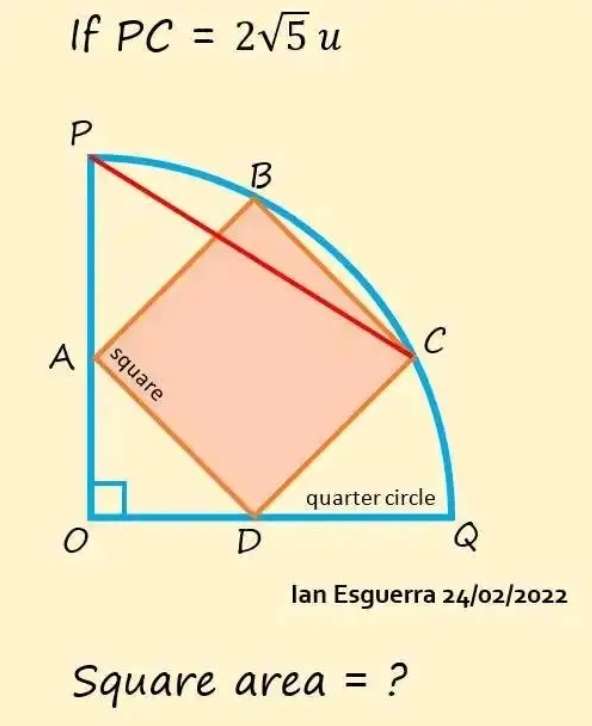
Mathematics Question and Solution
Let the inscribed square side length be a.
b² = 2a²
b = √(2)a units.
b is AC = BD, the diagonal of the inscribed square.
a² = 2c²
Where c is OA = OD.
c² = ½(a²)
c = √(a²/2)
c = ½(√(2)a) units.
d² = a²+(½(√(2)a))²-2a*½(√(2)a)cos135
d² = a²+½(a²)+a²
d² = 2a²+½(a²)
d² = ½(5a²)
d = √(2.5)a unit.
d is OP = OQ, the radius of the quarter circle.
e = √(2.5)a-½(√(2)a)
e = 0.8740320489a units.
e is AP = DQ.
Notice.
PC = 2√(5) units.
PC = 4.472135955 units.
Calculating a², area of the inscribed square.
(2√(5))² = (0.8740320489a)²+(√(2)a)²
20 = 0.7639320225a²+2a²
2.7639320225a² = 20
a² = 20/(2.7639320225)
a² = 7.2360679775 square units.
Again, a² is the area of the inscribed square.