Mathematics Question and Solution
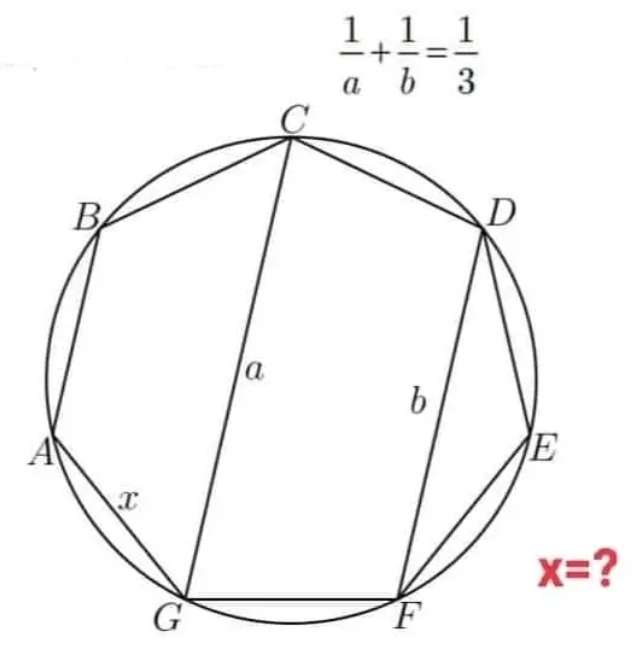
Calculating x, side length of the regular heptagon.
(1/a)+(1/b) = ⅓
3a+3b = ab
ab-3a = 3b
a(b-3) = 3b
a = 3b/(b-3) --- (1).
c = ⅐*180(7-2)
c = ⅐(900)°
c is the single interior angle of the regular heptagon.
d = 90-½*⅐(900)
d = ⅐(630-450)
d = ⅐(180)°
cos(⅐(180)) = ½(b)/x
x = 0.5549581321b
b = 1.8019377358x --- (2).
e = ½(360-⅐x2(900))
e = (180-⅐(900)
e = ⅐(1260-900)
e = ⅐(360)°
cos(⅐(360)) = f/x
f = 0.6234898019x units.
It implies;
a = x+2f
a = x+2(0.6234898019x)
a = 2.2469796037x --- (3).
Substituting (2) and (3) in (1) to get x.
a = 3b/(b-3)
2.2469796037x = 3(1.8019377358x)/(1.8019377358x-3)
2.2469796037x(1.8019377358x-3) = 5.4058132073x
4.0489173394x²-6.7409388111x = 5.4058132073x
4.0489173394x² = 12.1467520184x
x = 12.1467520184/4.0489173394
x = 3 units.
Again, x is the side length of the regular heptagon.
Therefore;
a = 2.2469796037x
a = 2.2469796037*3
a = 6.7409388112 units.
b = 1.8019377358x
b = 1.8019377358*3
b = 5.4058132074 units.
Checking Accuracy.
(1/6.7409388112)+(1/5.4058132074) = 0.3333333333
And;
0.3333333333 = ⅓
Checked.