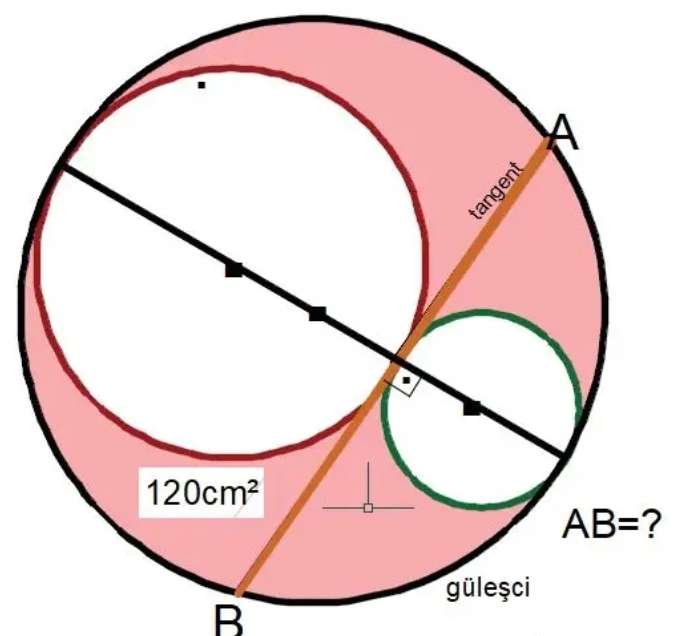
Mathematics Question and Solution
Let a be the radius of the big inscribed circle.
Let b be the radius of the bigger inscribed circle.
Therefore;
b = 2a cm.
c = 2a+a
c = 3a cm.
c is the radius of the ascribed circle.
It implies, calculating a.
120+π(2a)²+πa² = π(3a)²
120+4a²π+a²π = 9a²π
120 = 4a²π
a²π = 30
a² = (30*7)/22
a² = 105/11
a = √(105/11) cm.
a = 3.0895719033 cm.
b = 2a
And a = 3.0895719033 cm.
b = 6.1791438065 cm.
c = 3a
And a = 3.0895719033 cm.
c = 9.2687157098 cm.
Therefore;
a²+d² = c²
d² = c²-a²
d² = 9.2687157098²-3.0895719033²
d = 8.7386289751 cm.
Therefore;
AB = 2d
AB = 17.4772579501 cm.