
Calculating x (radius of the small inscribed circle)
28² + x² = (56-x)²
784 + x² = 3136 - 112x + x²
112x = 2351
x = 21 units.

a = 108-90
a = 18°
cos18 = b/1
b = 0.9510565163 units.
c = 1+0.9510565163
c = 1.9510565163 units.
c is the side length of the regular ascribed pentagon.
sin18 = d/1
d = 0.3090169944 units.
e² =...
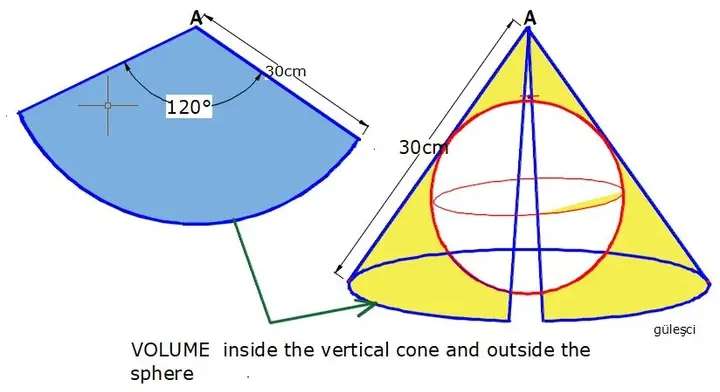
a = 120π*2*30÷360
a = ⅓(60)π
a = 20π cm.
a = 62.8318530718 cm.
a is the length of arc of the sector and also, the base circumference of the cone.
20π = 2πb
b = 10 cm.
b is the radius of th...
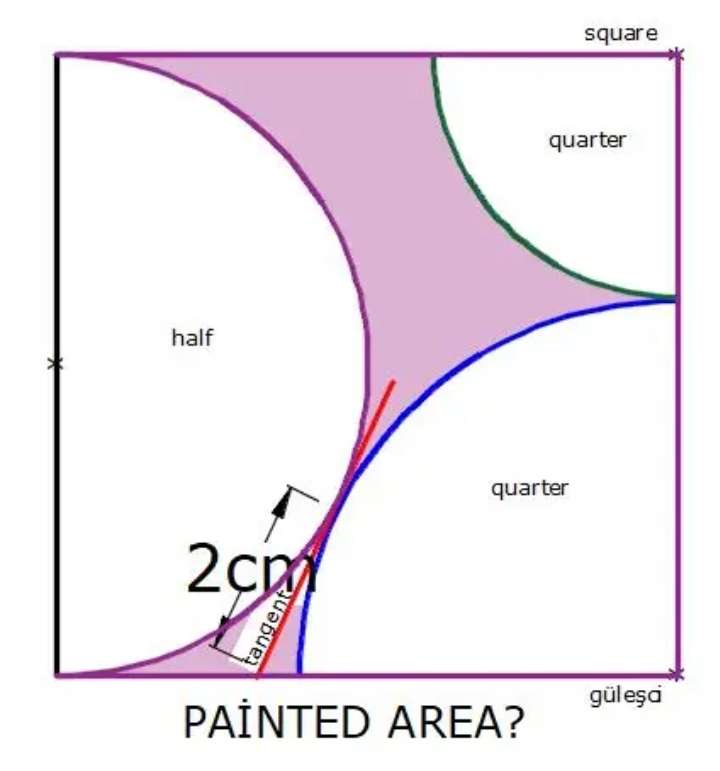
Let the square side be 2a cm.
It implies;
a is the radius of the inscribed semi circle.
Let b equal the radius of the big inscribed quarter circle.
Therefore;
(a+b)² = a²+(2a)²
a²+2ab...
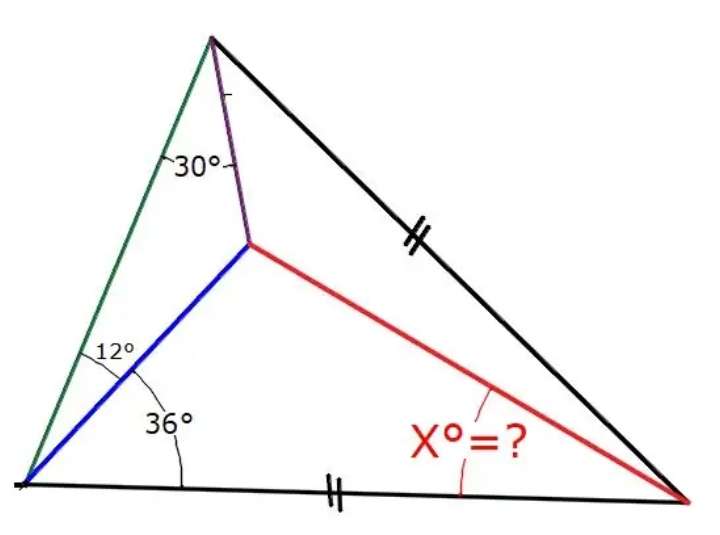
Let the two equal lengths of the isosceles triangle be 1 unit each.
a = 180-2(12+36)
a = 180-96
a = 84°
b² = 2-2cos84
b = 1.3382612127 units.
c = 180-12-30
c = 138°
(d/sin30) = (1.3...
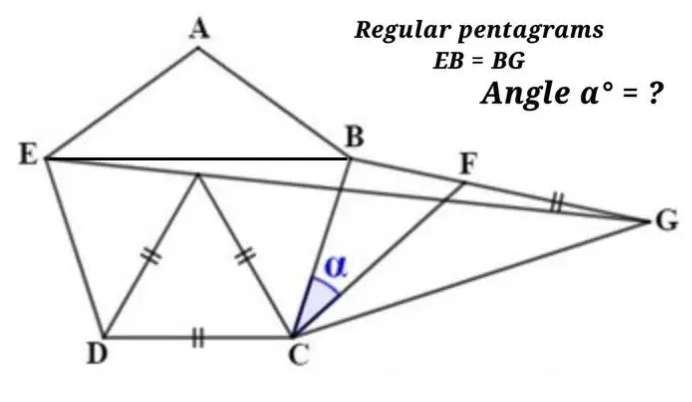
Let the side length of the regular pentagon be 1 unit.
a² = 2-2cos108
108° is the single interior angle of the regular pentagon.
a = 1.6180339887 units.
a is BE.
b = 108-60
b = 48°
c =...

a² = 3²+1²
a = √(10) units.
a is AB.
It implies;
AC = ½√(10) units.
tanb = 1/3
b = atan(1/3)°
tanc = ½√(10)/√(10)
c = atan(½)°
d² = (½√(10))²+√(10)²
d² = ½(5)+10
d = √(25/2)
d...

x+50+180-a = 180
a = x+50 --- (1).
x+30+180-b = 180
b = x+30 --- (2).
3x+180-2a+180-2b = 180
3x+180-2(a+b) = 0
2(a+b) = 3x+180 --- (3).
Therefore, substituting (1) and (2) in (3) to get...

tan30 = a/12
a = 12tan30
a = 4√(3) cm.
a is the side length of the square.
b = ½(12)+a
b = (6+4√(3)) cm.
c = ½(a)
c = 2√(3) cm.
Observing similar right-angled triangle side length rat...

Let x be the single interior angle of the regular polygon.
a = 180-x-20
a = (160-x)°
b = 180-x-30
b = (150-x)°
c = 180(5-2)
c = 540°
d = 2(360-x)°
It implies;.
a+b+d+86 = c
(16...