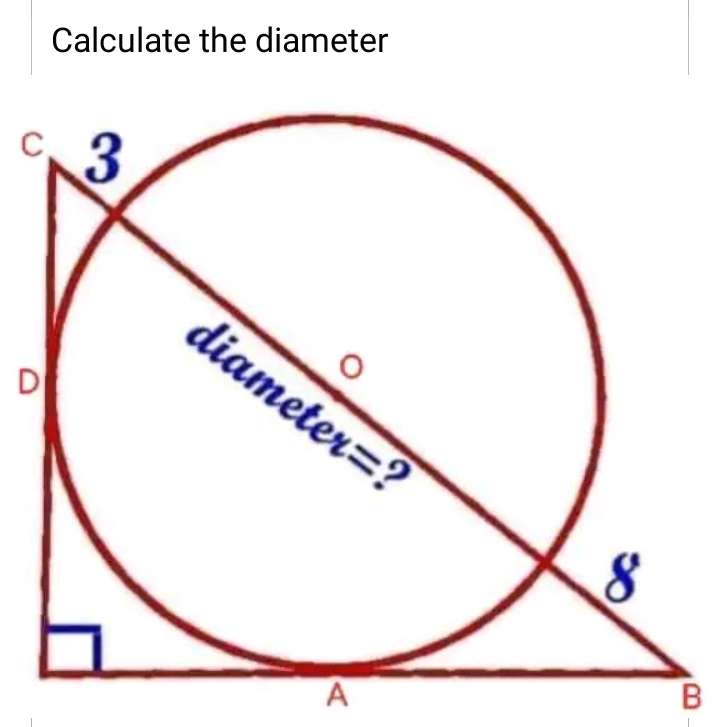
Let the radius of the circle be a.
b = (3+a) units.
c = (8+a) units.
d² = (3+a)²-a²
d = √(9+6a) units.
Observing similar plane shape (right-angled) side length ratios.
a - √(9+6a)...
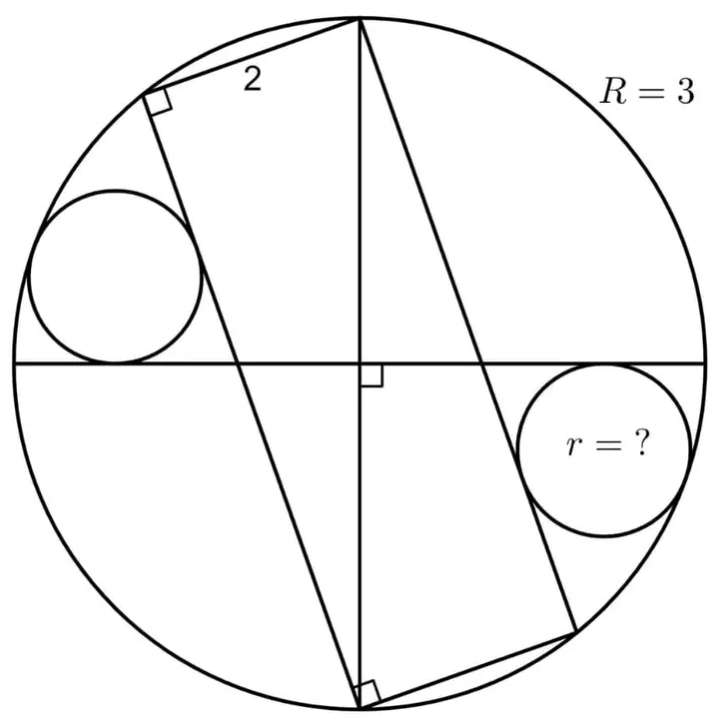
Diameter of the ascribed circle is;
2R
= 2*3
= 6 units.
a²+2² = 6²
a = √(32)
a = 4√(2) units.
Observing similar plane shape (right-angled) side length ratios.
3 - 4√(2)
b - 2
Cros...
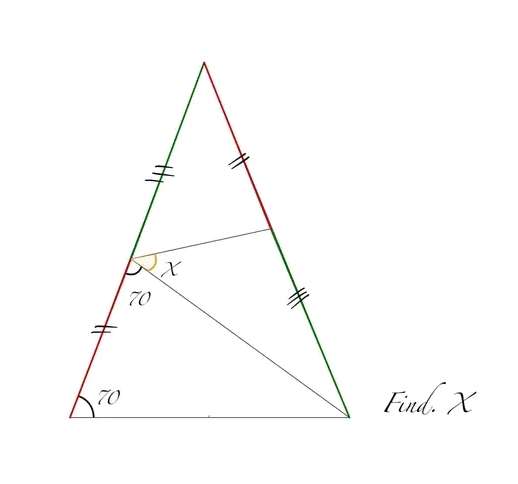
Let the base of the ascribed triangle be 1 unit.
a = 180-70-70
a = 40°
(b/sin40) = (1/sin70)
b = 0.6840402867 units.
Considering similar plane shape (isosceles triangle) side length rati...
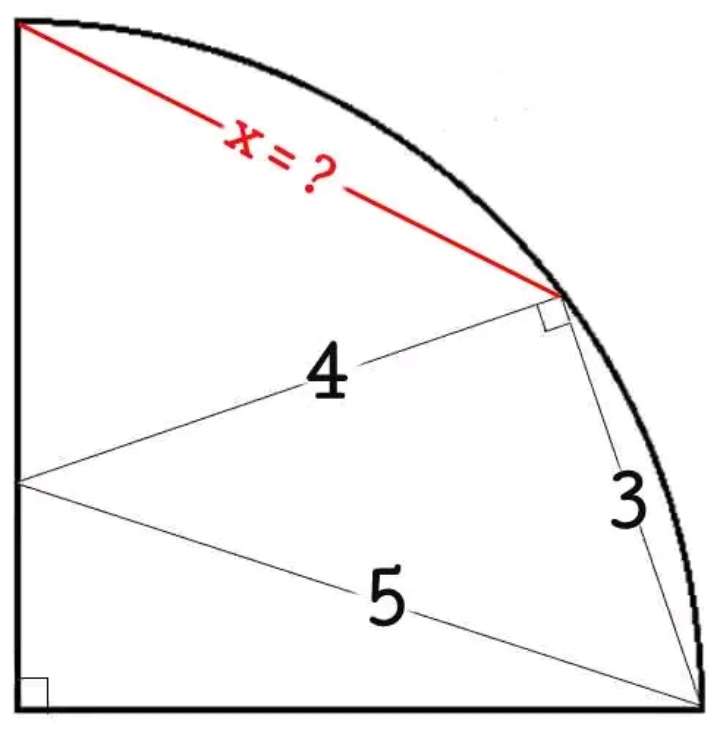
a = 4+5
a = 9 units.
b² = 9²+3²
b = √(90)
b = 3√(10) units.
c = ½(b)
c = ½(3√(10)) units.
c is the radius of the quarter circle.
d² = 5²-(½(3√(10)))²
d = √(25-(45/2))
d = √(½(5))
d...
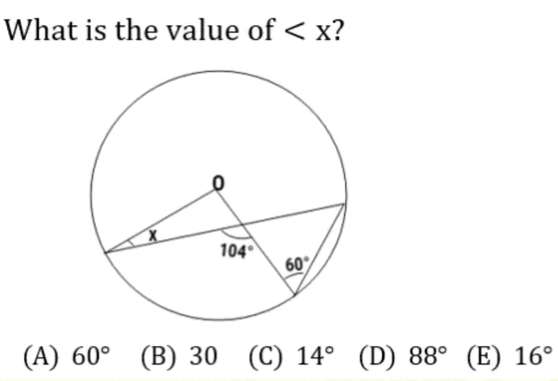
a = 180-(180-104)-60
a = 104-60
a = 44°
b = 2a
b = 88°
Calculating x, the required angle.
x = 180-88-(180-104)
x = 92-76
x = 16°
x is the required angle.
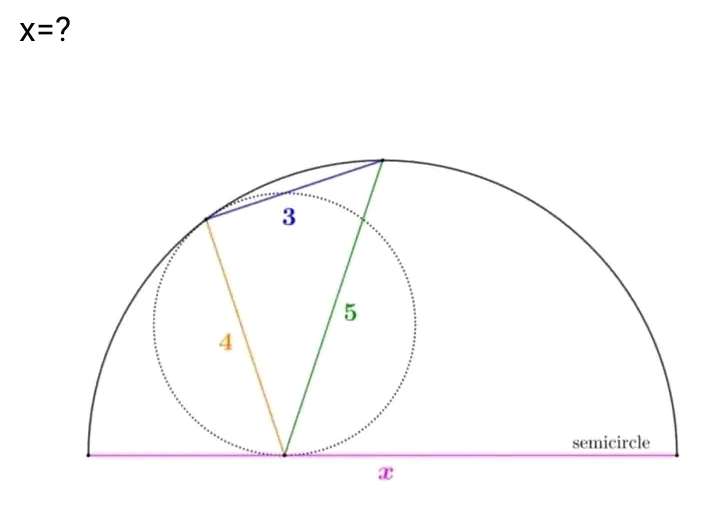
Let a be the radius of the ascribed semi circle.
tanb = (3/4)
b = atan(3/4)°
It implies;
3² = 2a²-2a²cos(atan(3/4))
9 = 2a²-(8a²/5)
9 = ⅕(2a²)
2a² = 9*5
a² = ½(9*5)
a = ½(3√(10)) uni...
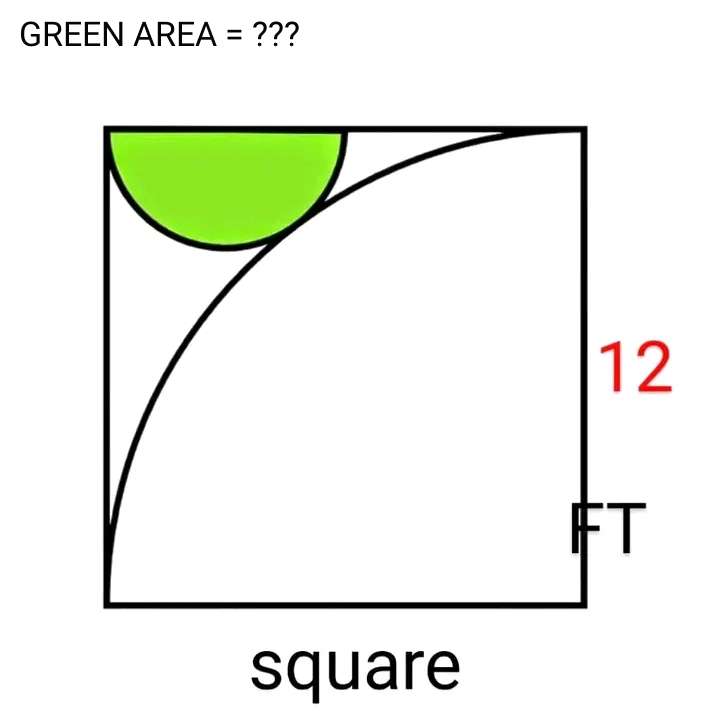
Let a be the radius of the inscribed half circle.
b = (12+a) units.
c = (12-a) units.
It implies;
(12+a)² = 12²+(12-a)²
144+24a+a² = 144+144-24a+a²
48a = 144
4a = 12
a = 3 units....
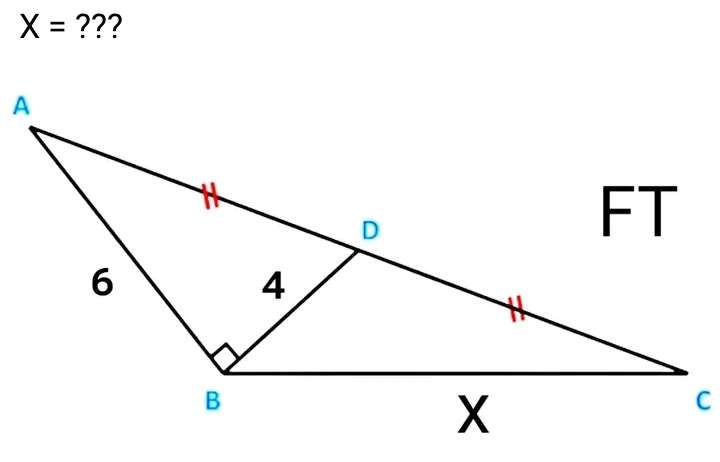
a² = 6²+4²
a = √(36+16)
a = √(52)
a = 2√(13) units.
a is AD = CD.
tanb = 6/4
b = atan(3/2)°
b is angle ADB.
c = 180-b
c = (180-atan(3/2))°
c is angle BDC.
Calculating x, length BC....
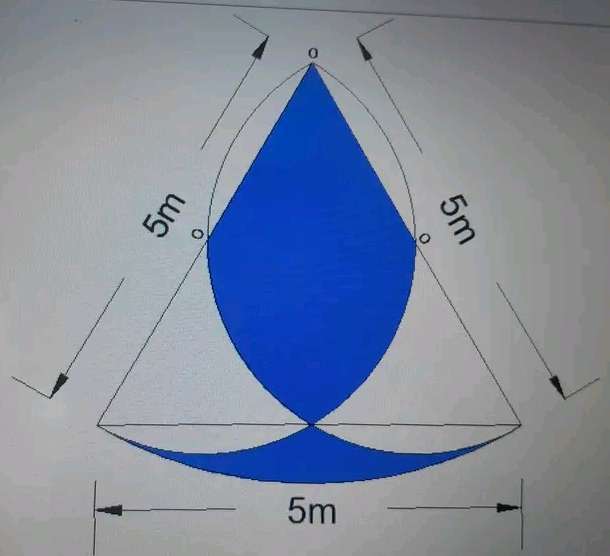
Calculating Area Red.
It is;
Area sector with radius 5 m and angle 60° - Area triangle with height 5 units and base 5sin60 m + 2(area triangle with height 2.5 m and base 2.5 m)
= (60π*5*5/...
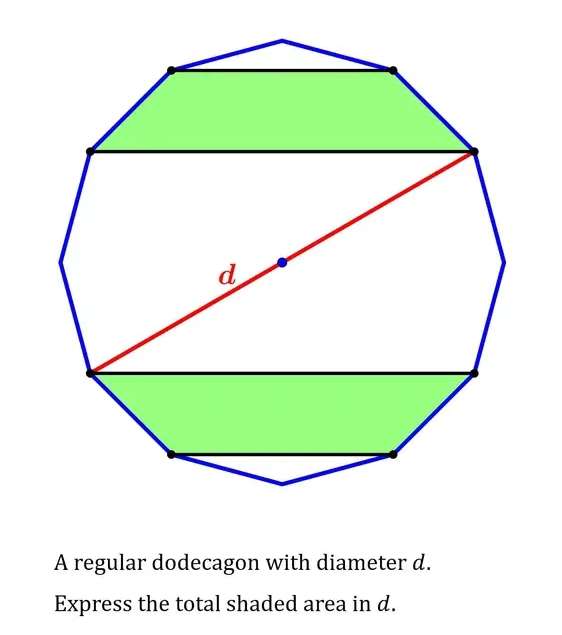
Calculating the total shaded area with respect to d.
a = (180(12-2))/12
a = 150°
a is the single interior angle of the regular dodecagon.
b = 105-75
b = 30°
sin30 = c/d
c = ½(d) units....