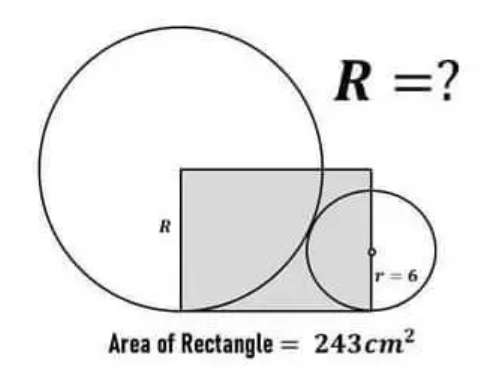
The width of the rectangle is;
R units.
The length of the rectangle is;
= √((R+6)²-(R-6)²)
= √(R²+12R+36-R²+12R-36)
= √(24R) units.
Therefore;
√(24R) * R = 243
24R³ = 243²
R³ = 2...
Please, move the above question left/right one time to review the solution.
Thank you.
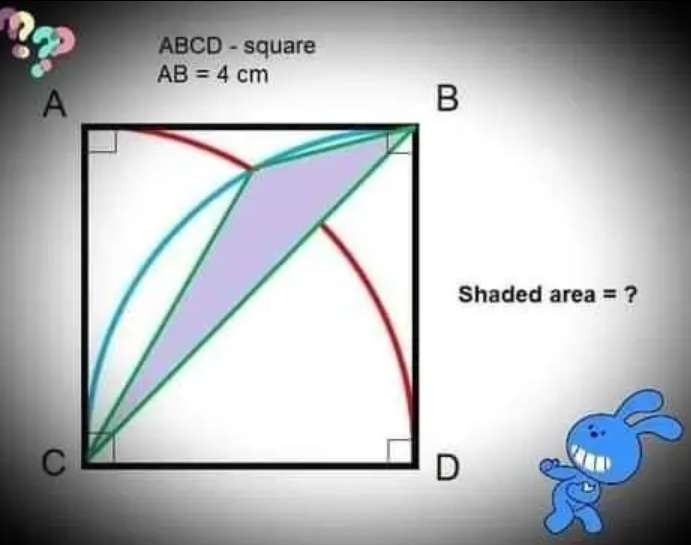
Area Shaded/blue or purple is;
= 8√(2)sin15 cm²
= 2.92820323028 cm²
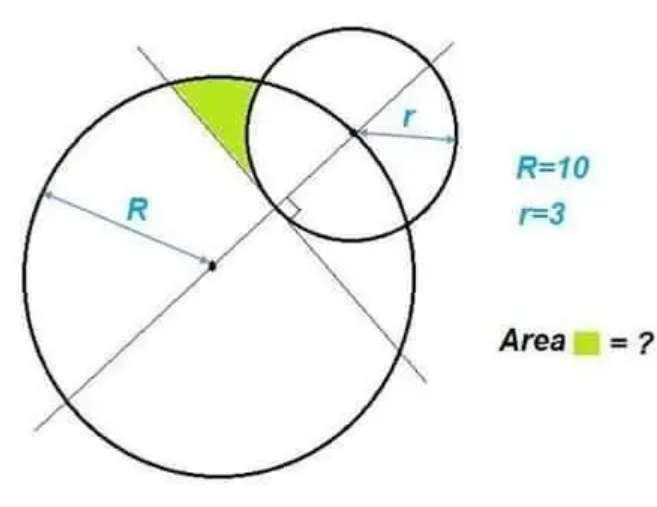
Shaded area is;
Area sector with radius 10 units and angle acos(0.7) - Area triangle with height √(51) units and base 7 units - area sector with radius 3 units and angle 81.37307344° - area sect...
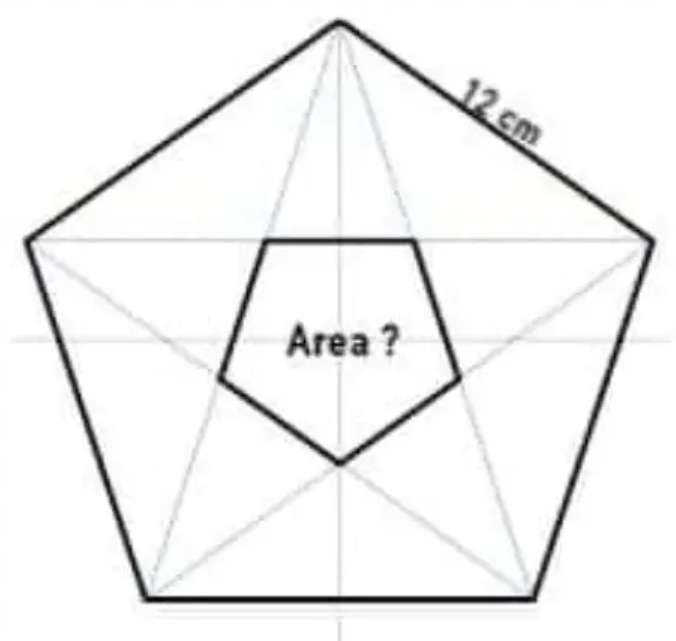
Calculating the area of the inscribed regular pentagon.
Let the single side length of the inscribed regular pentagon be x.
12²=2y²-2y²cos108
y = √(144/(2-2cos108))
y = 7.416407865 cm.
Ther...
Please, move the above question left/right one time to review the solution.
Thank you.
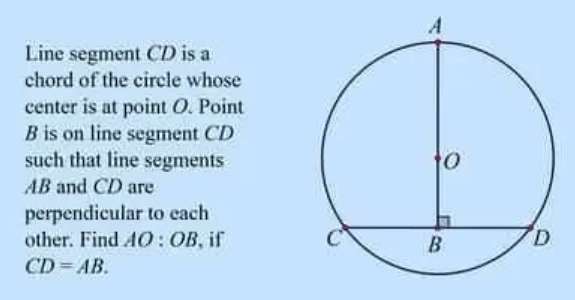
AO : OB is;
= 5 : 3
Sir Mike Ambrose is the author of the question.
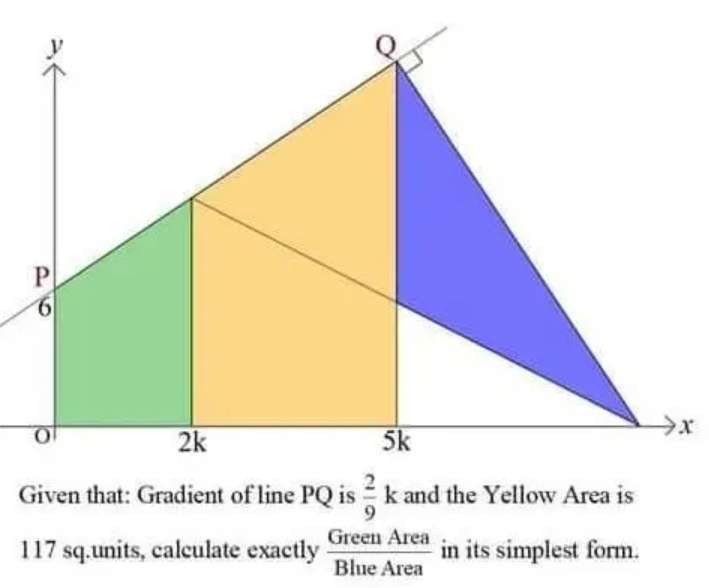
Calculating letter k considering yellow area (trapezoid).
It implies;
Half the sum of two parallel length (54+4k²)/9 units and (54+10k²)/9 units...
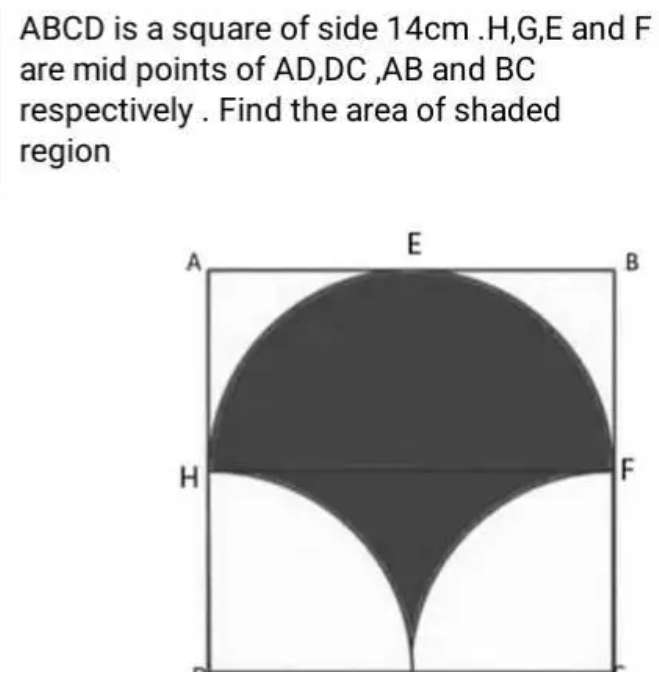
Shaded area is;
Area semi circle with radius 7cm + Area rectangle with length 14 cm and width 7 cm - Area semi circle with radius 7cm.
= ½(49π) + (14*7) - ½(49π)
= 98 cm²
Or
Shaded Area...
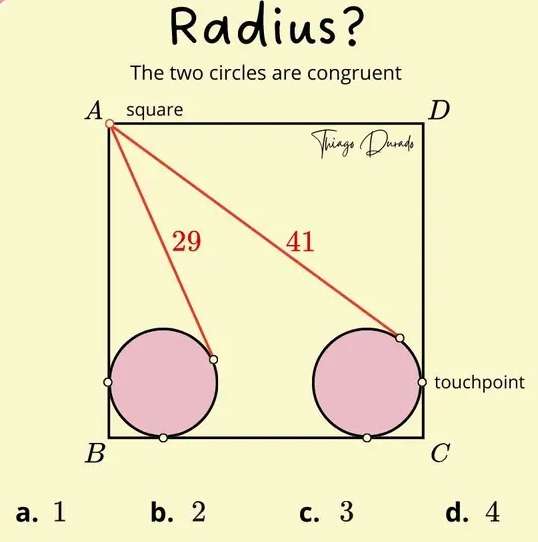
Let a ber the radius of each of the two congruent circles.
b = (a+29) units.
b is the side length of the square.
c² = 2*29²
c² = 1682
c = 29√(2) units.
Calculating a.
It implies;...
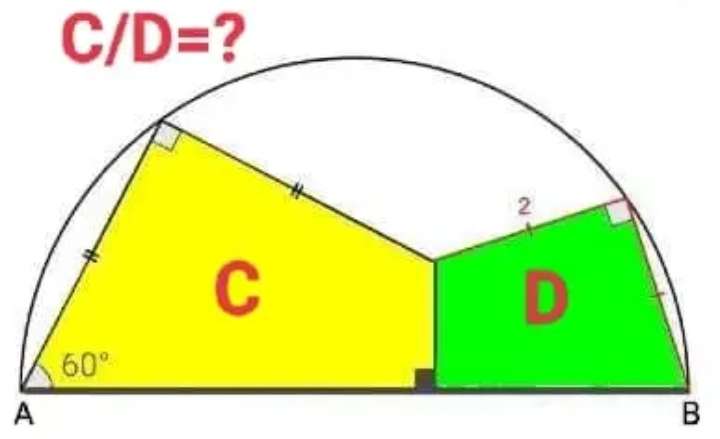
Calculating green area.
a² = 2²+2²
a = √(8)
a = 2√(2) units.
sin30 = b/a
½ = b/(2√(2))
b = √(2) units.
c²+b² = a²
c²+√(2)² = (2√(2))²
c² = 8-2
c = √(6) units.
Area green is;
(...
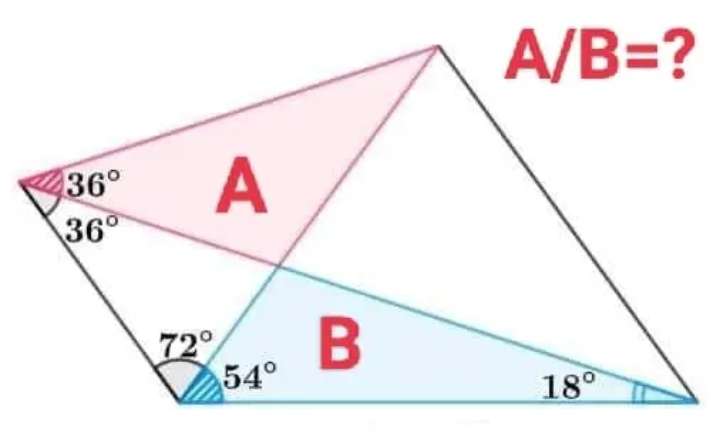
Let the base of the quadrilateral be 1 unit.
a = -54-18+180
a = 108°
(1/sin108) = ((b/sin18)
b = 0.3249196962 units.
Therefore, area B is;
0.5*1*0.3249196962sin54
= 0.131432778 squar...