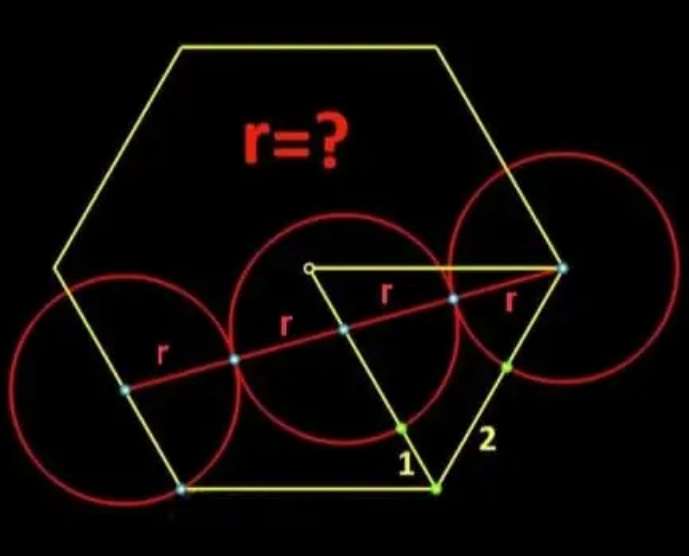
Calculating r.
a = (2+r) units.
b = (1+r) units.
c = r+r
c = 2r units.
It implies;
(2r)² = (1+r)²+(2+r)²-2(1+r)(2+r)cos60
4r² = 1+2r+r²+4+4r+r²-(2+3r+r²)
4r² = 2r²+6r+5-2-3r-r²
3...
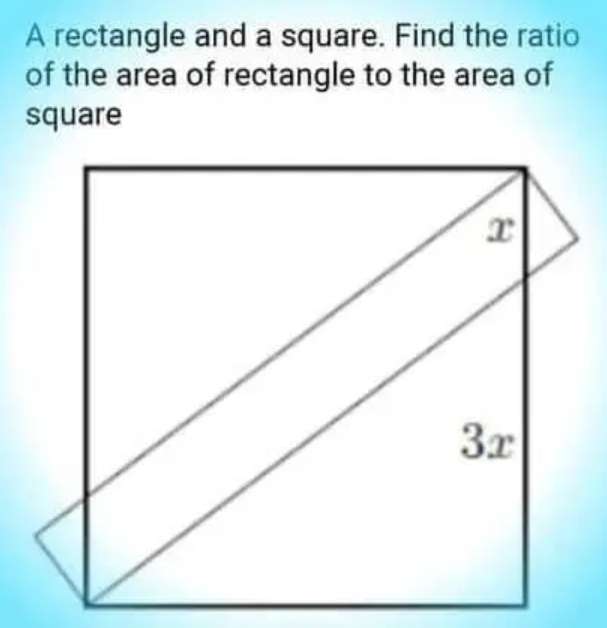
Let x be 2 units.
Therefore;
Area square is;
8²
= 64 square units.
Calculating area rectangle.
The length is;
√(8²+6²) + 2cos(atan(4/3))
= 10+(6/5)
= 56/5 units.
The width i...
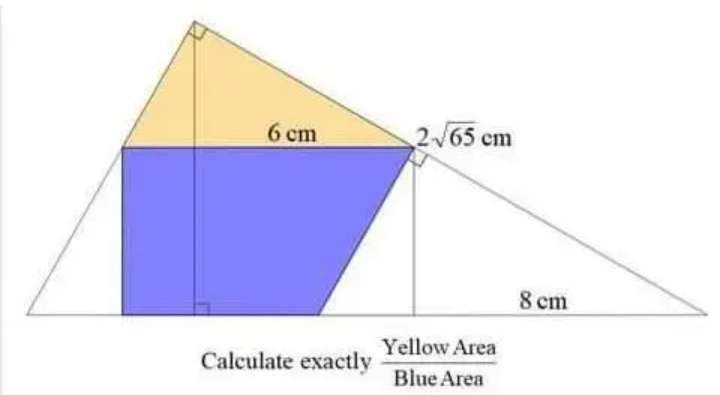
Area yellow is;
Area triangle with two side (6√(65)/7) cm and 7.95918367347 cm, and angle acos(7/√(65))°
= ½*(6√(65)/7)*7.95918367347sin(acos(7/√(65)))
= 13.6443148688 cm²
Area blue is;...
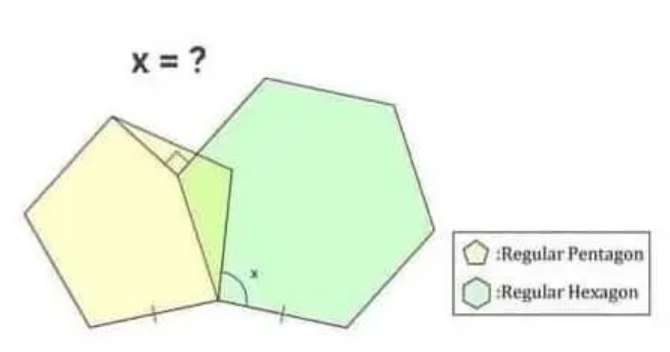
a = ⅕*180(5-2)
a = 108°
a is the single interior angle of the regular pentagon.
b = ⅙*180(6-2)
b = 120°
b is the single interior angle of the regular hexagon.
c+90+(180-30)+2(108) = 180(5...
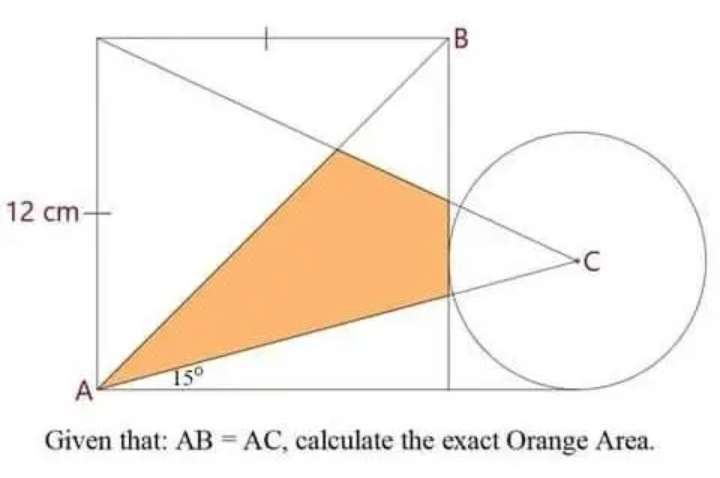
Sir Mike Ambrose is the author of the question.
Area orange exactly in its decimal form is;
Half area square with side 12 units - Area triangle with height 12 units and base 12tan15 units - Are...
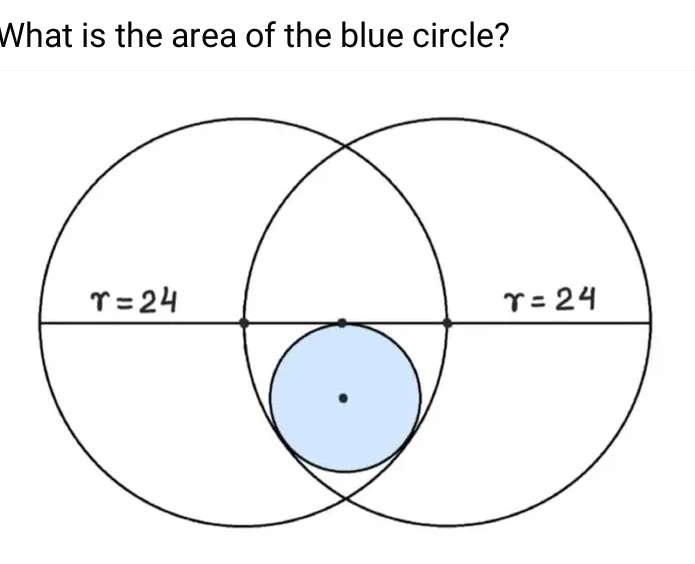
Let a be the radius of the inscribed blue circle.
b = (24-a) units.
c = ½(24)
c = 12 units.
Therefore, Calculating a.
a²+12² = (24-a)²
a²+144 = 576-48a+a²
48a = 432
a = 9 units.
Ag...
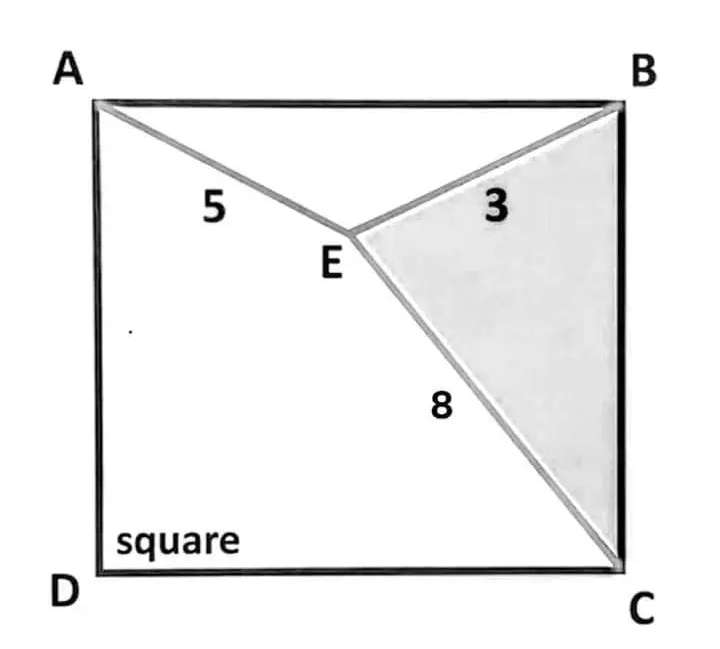
Calculating shaded area (triangle BCE).
Let a be the side length of the square.
5² = a²+3²-2*3*acosb
25 = a²+9-6acosb
16 = a²-6acosb --- (1).
8² = a²+3²-2*3*acos(90-b)
64 = a²+9-6a(cos9...
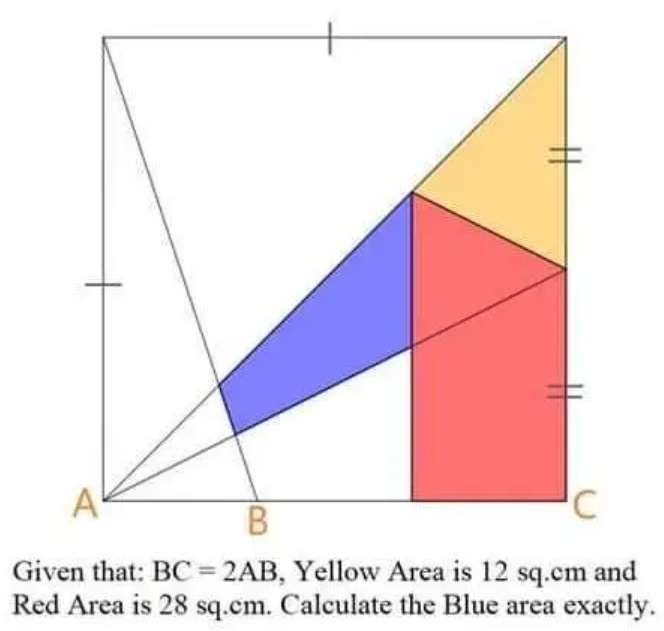
Sir Mike Ambrose is the author of the question.
Notice;
The single side length of the square is 12 units.
Area blue is;
Area triangle with height and base 8 units each - Area triangle wit...
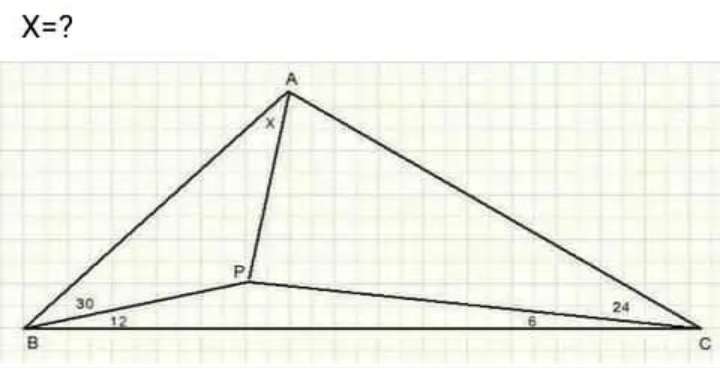
Please, move the above question left/right one time to review the solution.
Thank you.
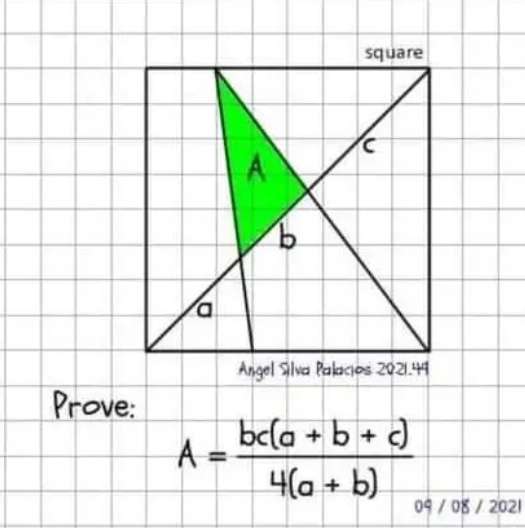
Please, move the above question left/right one time to review the solution.
Thank you.