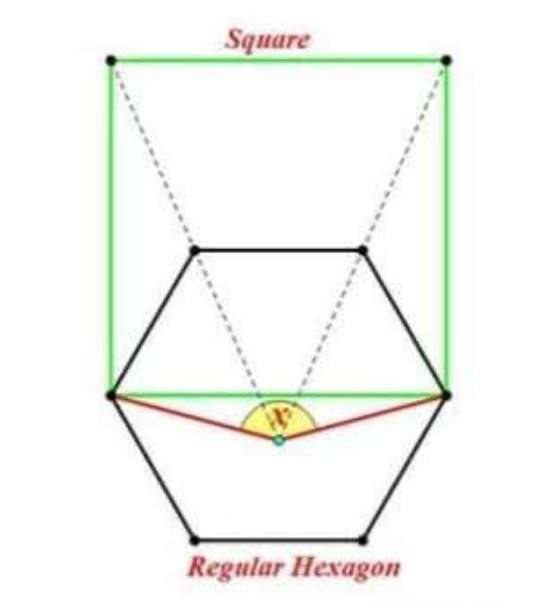
Let the side length if the regular hexagon be 1 unit.
Therefore the side length of the square, y is;
½+1+½
y = 2 units.
It implies;
The yellow shaded angle, x is;
(180 - 2atan(2-√...

Let the side of the regular pentagon be 1 unit.
a = 108-90
a = 18°
b = 180-108-18
b = 54°
(1/sin54) = (c/sin108)
c = 1.17557050458 units.
(1/sin54) = (d/sin18)
d = 0.38196601125 un...
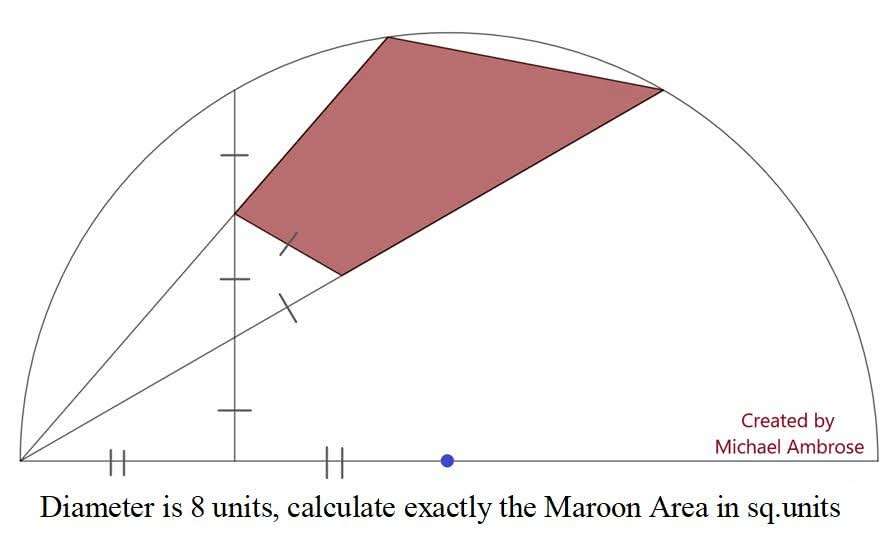
Notice;
The diameter of the semicircle is 8 units.
Therefore radius is 4 units.
tan30 = a/2
a = ⅔(√(3)) units.
b = 3a
b = 2√(3) units.
c² = 2²+(⅔(√(3)))²
c = (4/√(3)) units.
d...
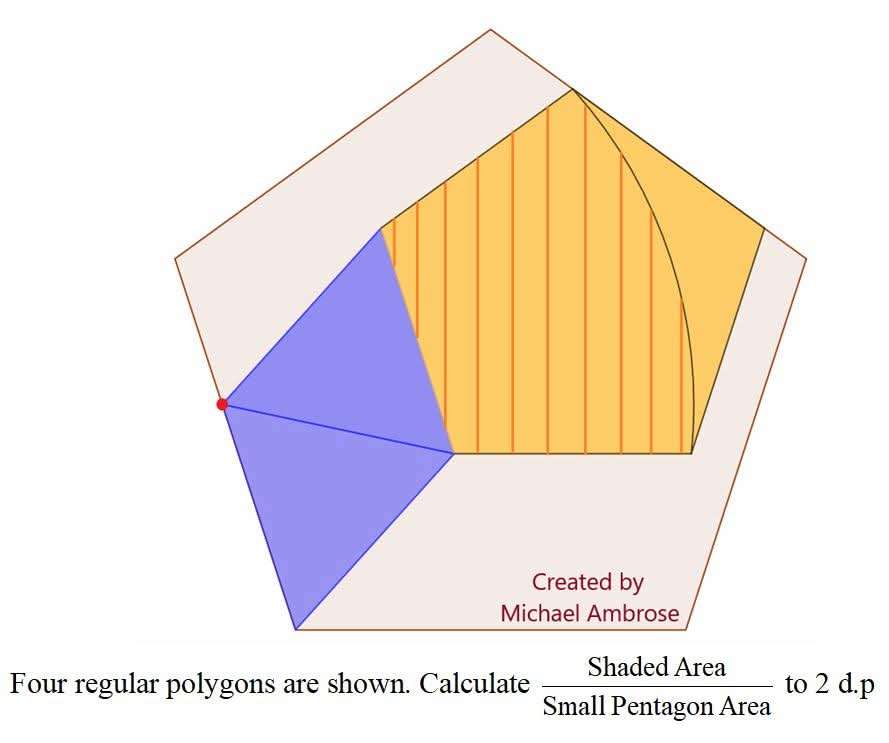
Let the inscribed regular pentagon side be 1 unit.
Area small/inscribed pentagon is;
0.5*5(1/(2tan(180/5)))
= 1.72047740059 square units.
Calculating Shaded Area.
a² = 2-2cos(60+108)...
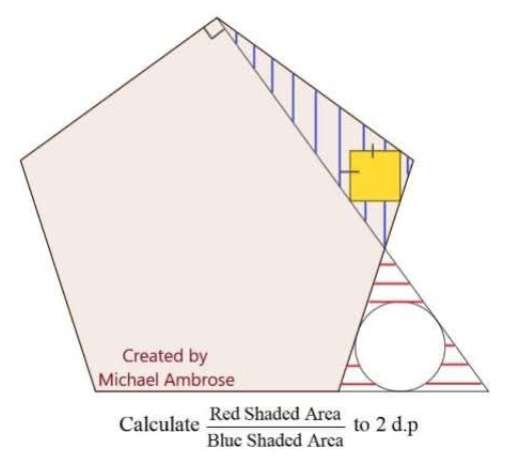
Let the side of the regular pentagon be 1 unit.
a = 360-2(108)-90
a = 54°
tan72 = b/0.5
b = 1.53884176859 units.
tan54 = 1.53884176859/c
c = 1.11803398875 units.
d = c-0.5
d = 0.618...

Let the single side length of the two congruent inscribed regular pentagon be 1 unit.
Area Green is;
0.5*5(1/(2tan(180/5)))
= 1.72047740059 square units.
Calculating Area Shaded.
a = ⅕...
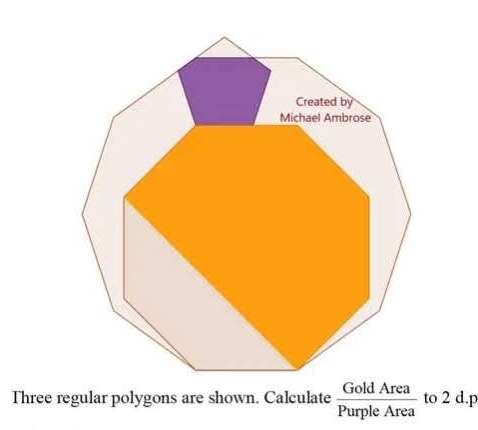
Let the side of the regular decagon which is equal the side of the regular octagon be 1 unit.
Calculating Area Gold.
a = ⅛(180*6)
a = 135°
b = ½(360-2(135))
b = 45°
sin45 = c/1
c = ½...
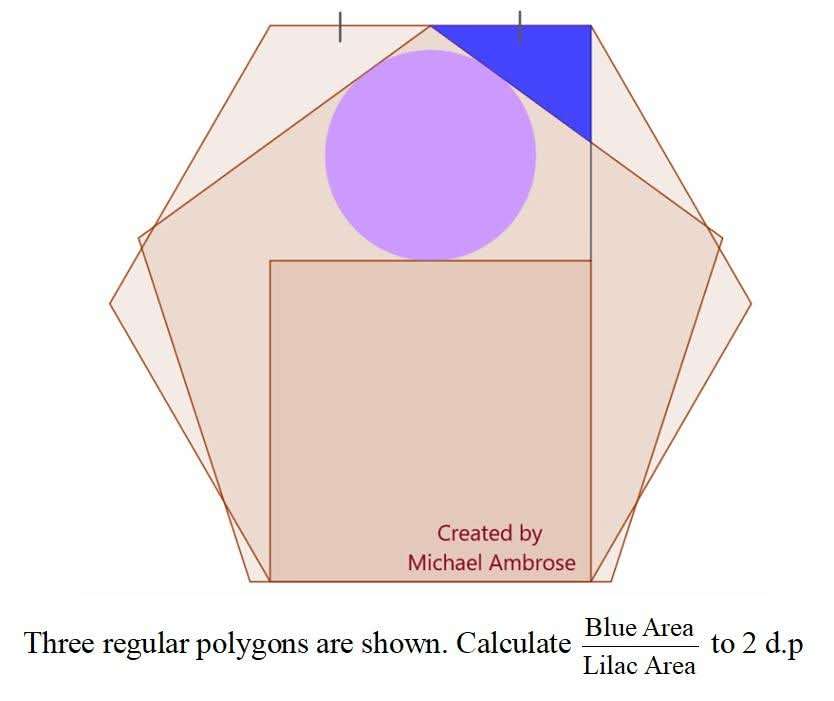
Let the side of the regular hexagon which is equal the side of the square be 1 unit.
a = ½(180-108)
a = 36°
tan36 = b/0.5
b = 0.363271264 units.
Area Blue is;
0.5*0.363271264*0.5
= 0...
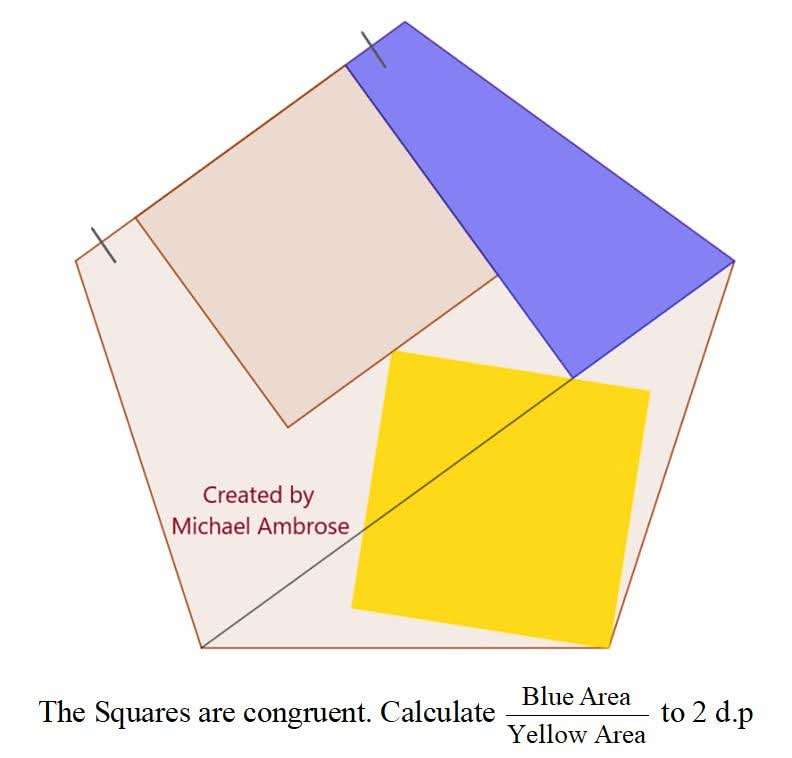
Let the regular pentagon side be 1 unit.
sin72 = a/1
a = 0.9510565163 units.
Let the side of the two inscribed congruent squares be b.
c = ½(b) units.
b+½(b) = 0.9510565163
b = 0.6340...
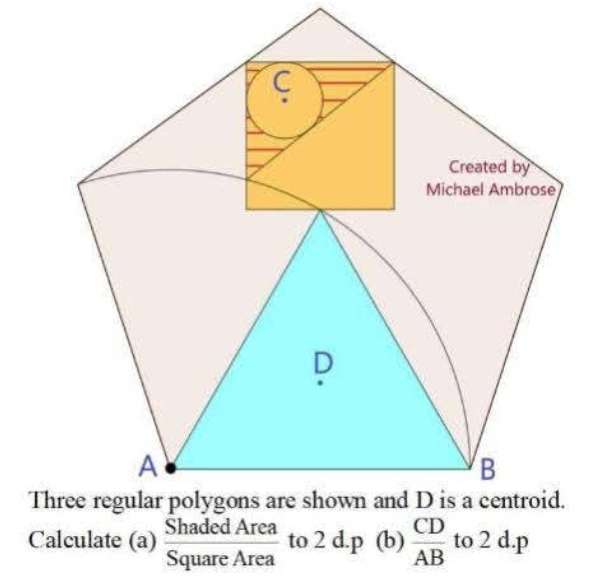
Let the side of the regular pentagon be 1 unit.
a² = 2-2cos108
a = 1.61803398875 units.
sin30 = b/0.5
b = 0.25 unit.
c = 2b
c = 0.5 unit.
Where c is the inscribed square side.
Are...