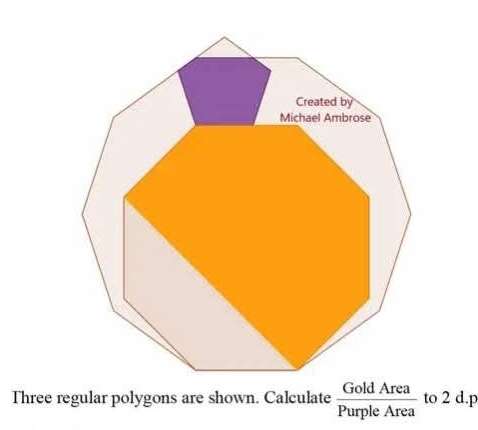
Mathematics Question and Solution
Let the side of the regular decagon which is equal the side of the regular octagon be 1 unit.
Calculating Area Gold.
a = ⅛(180*6)
a = 135°
b = ½(360-2(135))
b = 45°
sin45 = c/1
c = ½(√(2)) units.
d = 1+2c
d = (1+√(2)) units.
Area Gold is;
Area regular octagon with side 1 unit - Area trapezoid with parallel sides 1 unit and (1+√(2)) units, and height ½(√(2)) units.
= ½(8*1)*(1/(2tan(180/8))-0.5(1+1+√(2))*(√(2)/2)
= 4.82842712475-1.20710678119
= 3.62132034356 square units.
Calculating Area Purple.
e = ⅒(180*8)
e = 144°
f = ½(144)
f = 72°
tan72 = g/1
g = 3.07768353718 units.
h = g-d
h = 0.6634699748 units.
(0.6634699748/sin108) = (i/sin54)
i = 0.56438127038 units.
Where i is the side length of the regular pentagon.
Area Purple is;
Area rectangle with height and base 0.6634699748 units and 0.56438127038 units respectively + 2(Area triangle with height 0.56438127038 units and base 0.6634699748sin18° units).
= 0.6634699748*0.56438127038+2(0.5*0.56438127038*0.6634699748sin18)
= 0.4901614492 square units.
Area Gold ÷ Area Purple to 2 decimal places is;
3.62132034356÷0.4901614492
= 7.3880154171
≈ 7.39