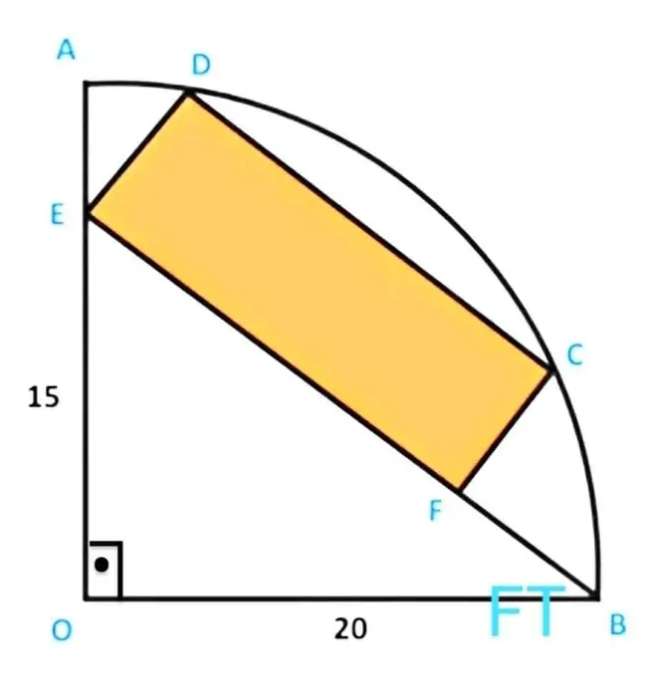
Calculating area inscribed yellow rectangle.
tana = 20/15
a = atan(4/3)
b = 90+a
b = (90+atan(4/3))°
(20/sin(90+atan(4/3))) = (15/sinc)
c = 26.7436839504°
d = 180-(90+atan(4/3))-26.7...
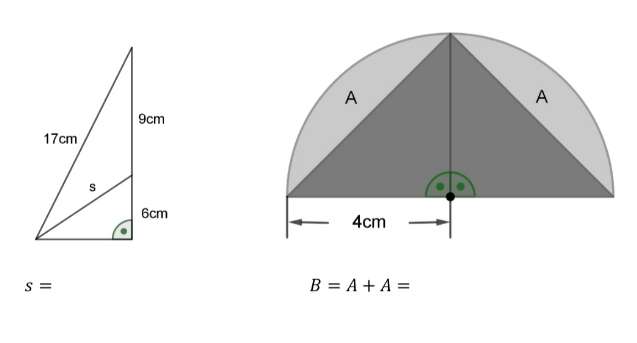
1. The Right-angled Triangle.
Calculating length x.
a = 9+6
a = 15 cm.
a is the height of the ascribed right-angled triangle.
17 cm is the hypotenuse of the ascribed right-angled triangl...
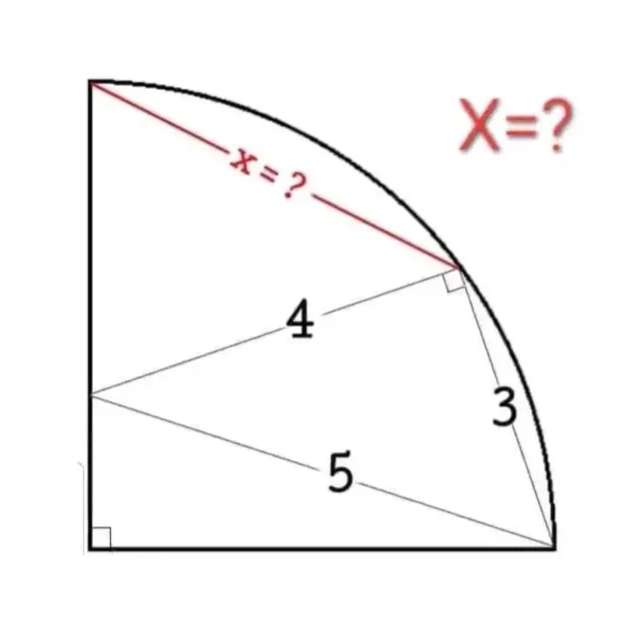
Let the radius of the quarter circle be a.
b = 2a units.
c = 4+5
c = 9 units.
It implies;
3²+9² = (2a)²
4a² = 90
a² = ½(45)
a = ½(3√(10)) units.
a = 4.7434164903 units.
Again, a i...
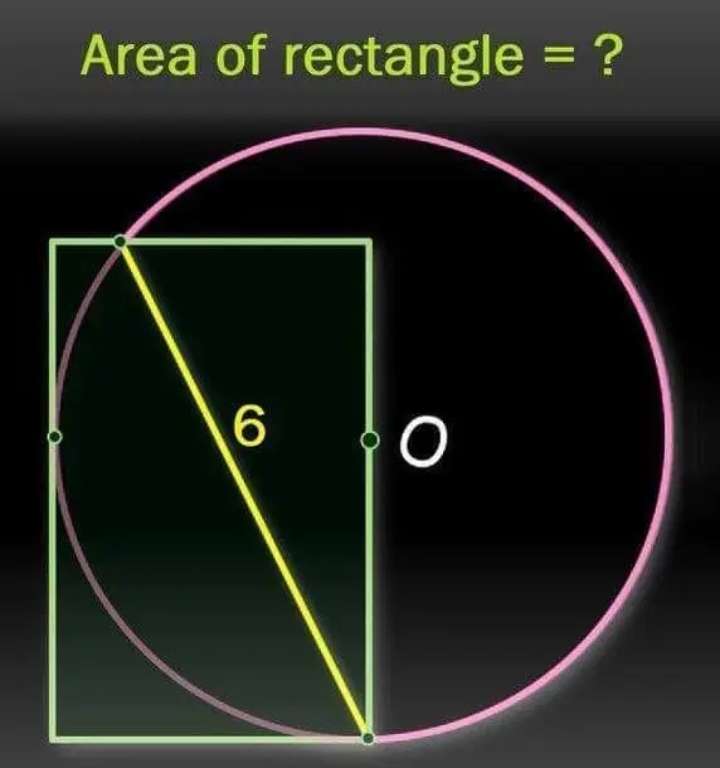
Let a be the radius of the circle.
tanb = (0.5a)/a
b = atan(0.5)°
cos(atan(0.5)) = c/6
c = 5.366563146 units.
sin(atan(0.5)) = d/6
d = 2.683281573 units.
cosatan(0.5) = 3/a
a = 3.35...
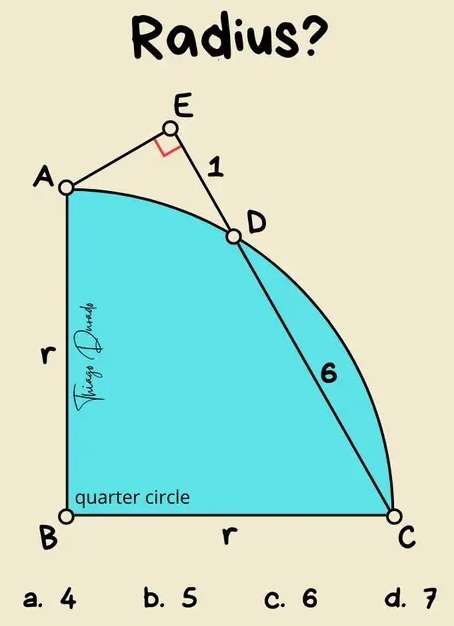
Calculating r, radius of the quarter circle
Notice.
AE = DE = 1 unit.
CE = 6+1
CE = 7 units.
AC = √(2r²)
AC = √(2)r units.
It implies;
(√(2)r)² = 7²+1²
2r² = 50
r = √(25)
r...
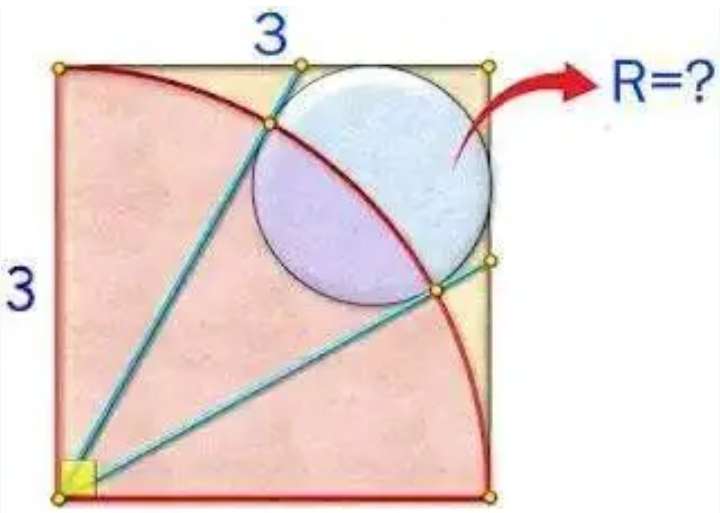
Calculating R, radius of the inscribed circle.
a² = 2*3²
a = 3√(2) units.
a is the diagonal of the square.
b² = 2R²
b = √(2)R units.
c = a-b
c = (3√(2)-√(2)R) units.
It implies;...
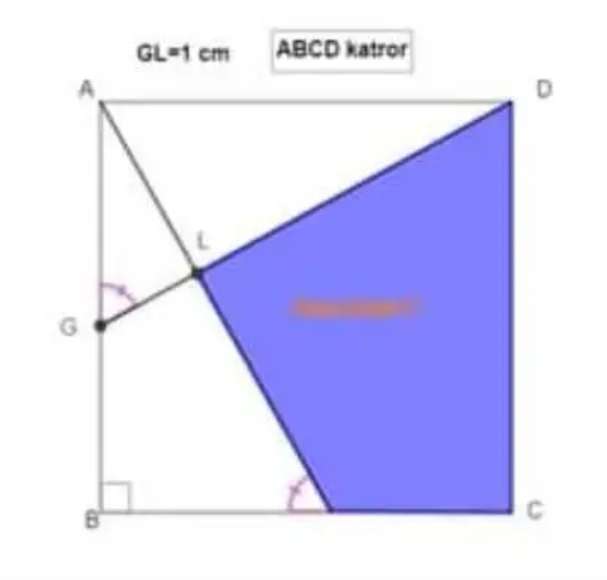
The single side length of the square, ABCD is;
2√(5) cm
Area Blue is;
Area square with length 2√(5) cm - area triangle with height 2√(5) cm and base √(5) cm - area triangle with height 4cm...
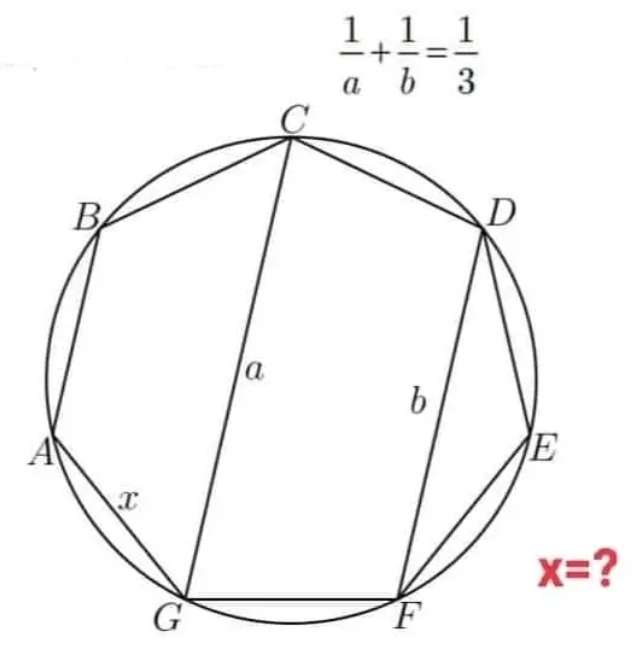
Calculating x, side length of the regular heptagon.
(1/a)+(1/b) = ⅓
3a+3b = ab
ab-3a = 3b
a(b-3) = 3b
a = 3b/(b-3) --- (1).
c = ⅐*180(7-2)
c = ⅐(900)°
c is the single interior angle of the...
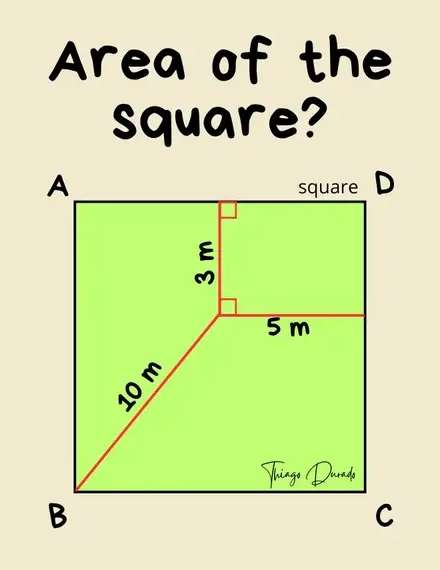
Let a be the side length of the square.
b = (a-3) m.
c = (a-5) m.
It implies;
10² = (a-3)²+(a-5)²
100 = a²-6a+9+a²-10a+25
2a²-16a+34-100 = 0
2a²-16a-66 = 0
a²-8a-33 = 0
a²-11a+3a-3...
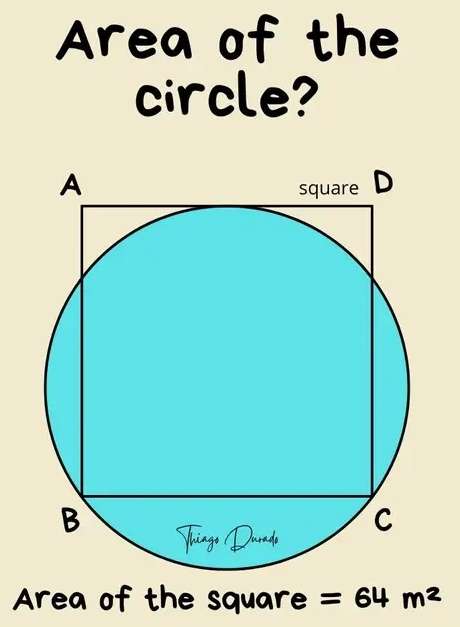
a² = 64
a = 8 m.
a is the side length of the square.
Calculating radius of the circle.
b = ½(8+c) m.
b is the radius of the circle.
d = ½(8-c) m.
Therefore;
(½(8+c))² = (½(8-c))²+...