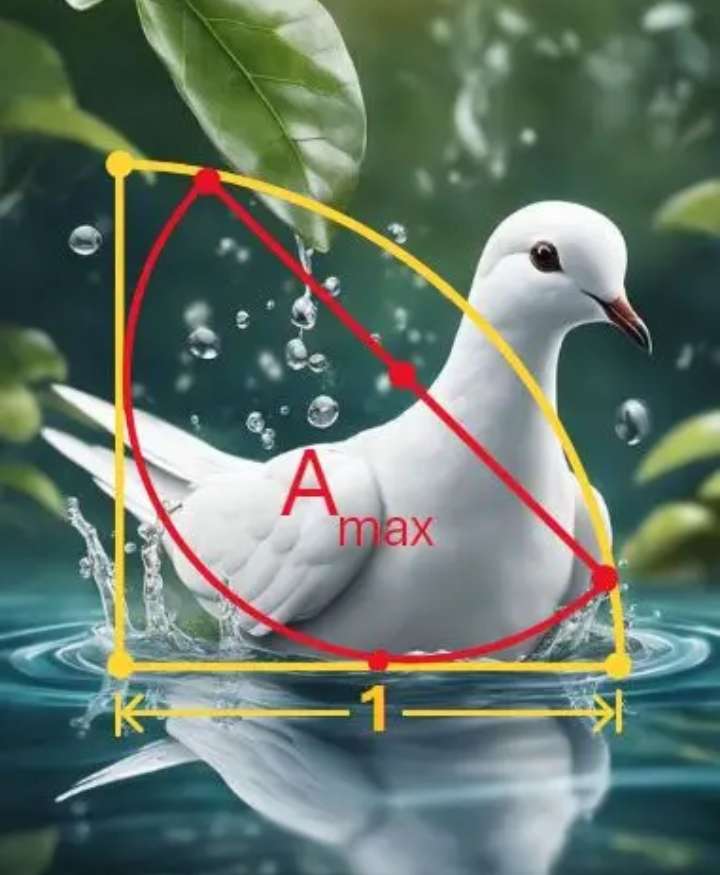
Calculating Area of the inscribed half circle.
Let the radius of the inscribed half circle be a.
b² = 2a²
b = √(2)a units.
It implies;
1² = a²+b²
1 = a²+(√(2)a)²
1 = a²+2a²
a² = ⅓...
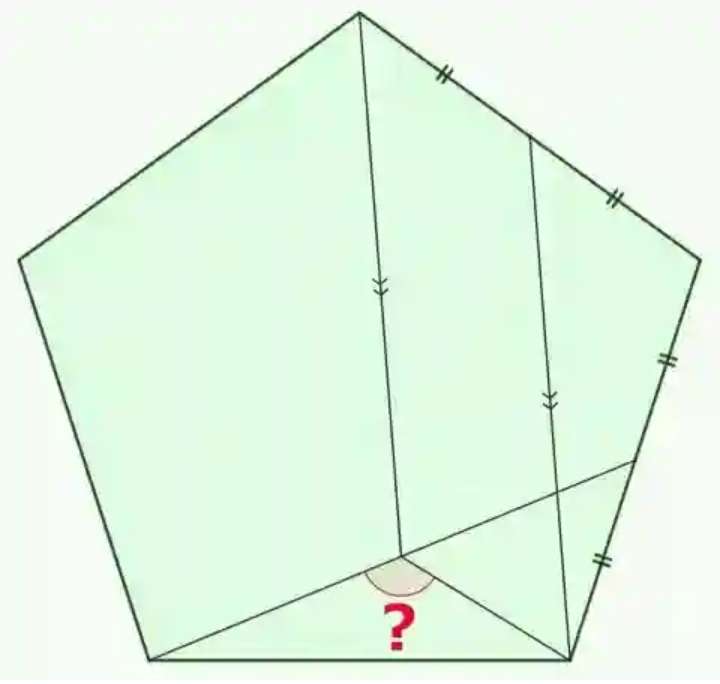
Let the side length of the ascribed regular pentagon be 2 units.
a = ⅕*180(5-2)
a = 108°
a is the single interior angle of the ascribed regular pentagon.
b² = 2²+1²-2*1*2cos108
b = 2.49721...
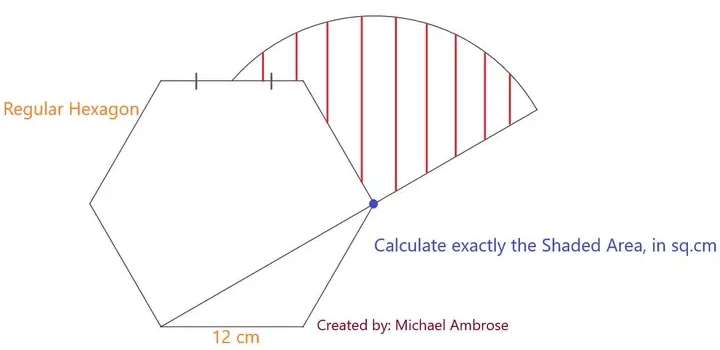
a = ½(12) cm.
a = 6 cm.
b = ⅙*180(6-2)
b = 120°
b is the single interior angle of the regular hexagon.
c² = 6²+12²-2*6*12cos120
c = 15.8745078664 cm.
c = 6√(7) cm.
c = 15.8745078664 cm....
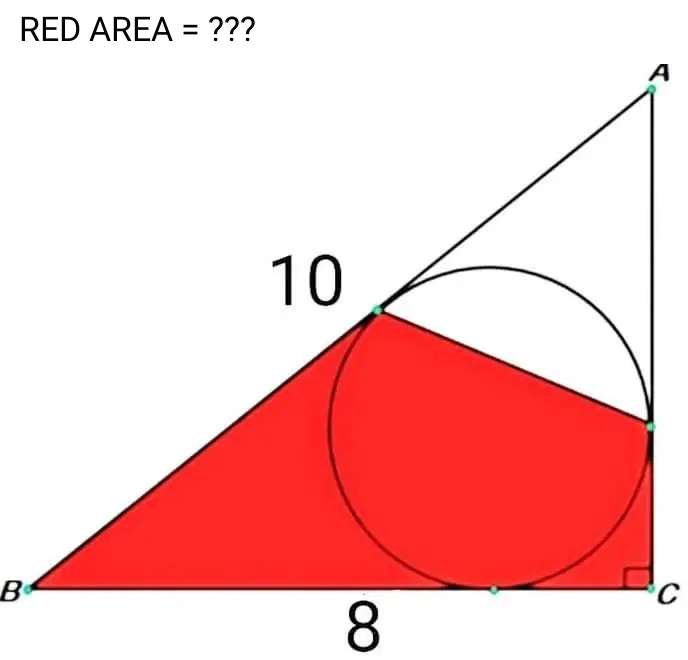
a²+8² = 10²
a = 6 units.
a is AC,the height of triangle ABC.
Calculating b, radius of the inscribed circle.
10b+8b+6b = 8*6
24b = 48
b = 2 units.
c = 6-b
c = 4 units.
d = 8-b
d =...
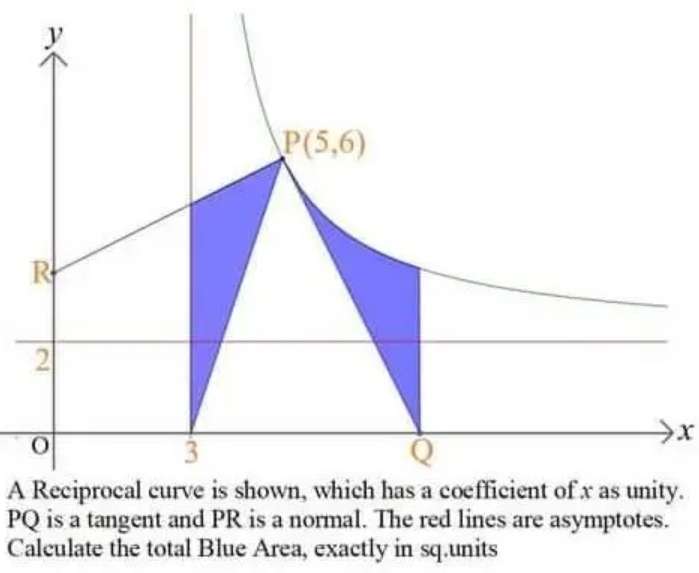
Sir Mike Ambrose is the author of the question.
The equation of the curve is;
y = (8/(x-3)) + 2
Area blue is;
Area trapezoid with two parallel side 5 units and 6 units, and height 2 units -...
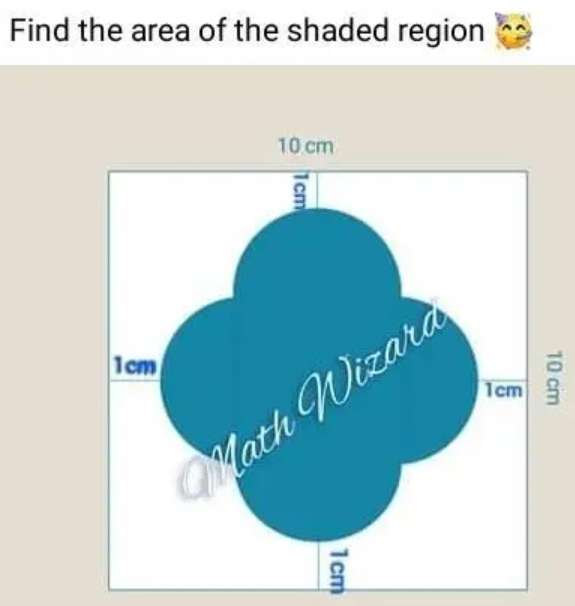
Blue area is;
2(area circle with radius 2 cm) + Area square with single side length 4 cm.
= 2(4π) + 16
= 8π + 16
= 8(π+2) cm²
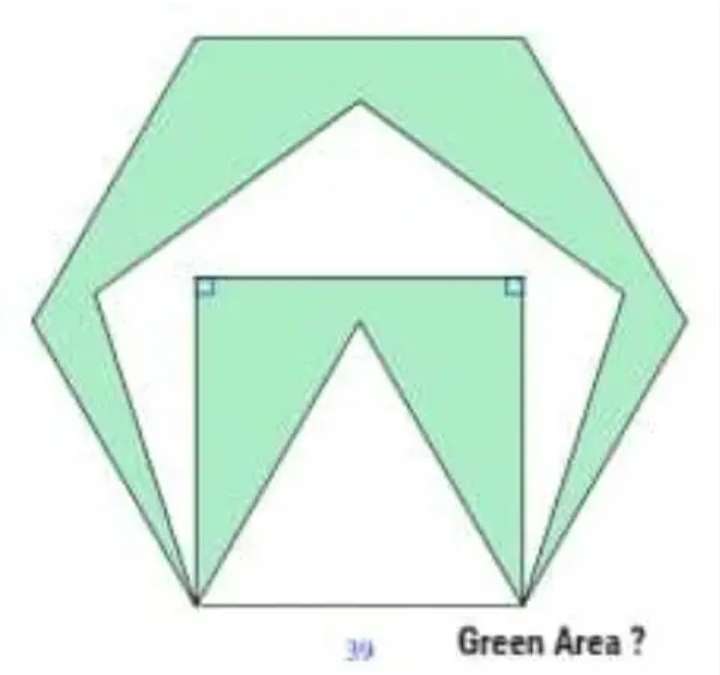
Notice;
The single side length of the ascribed regular hexagon, the inscribed regular pentagon, the inscribed square, and the inscribed equilateral triangle are equal.
It is 39 units.
Ther...
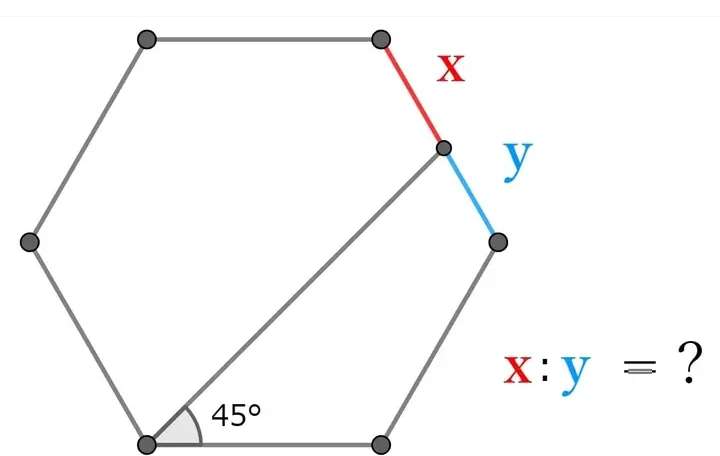
Let the side length of the regular hexagon be 1 unit.
It implies;
x+y = 1
a = ⅙*180(6-2)
a = 120°
a is the single interior angle of the regular hexagon.
b = 360-2a-45
b = 360-285
b...
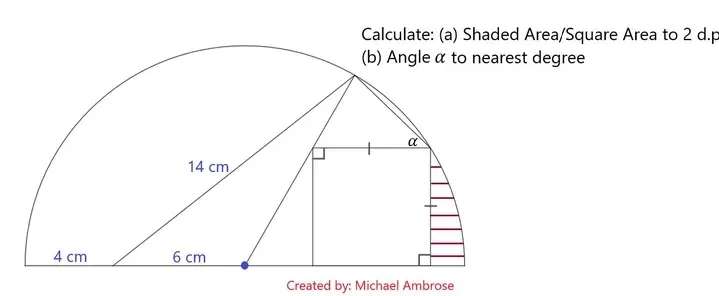
Let the side length of the inscribed square be a.
b² = 2a²
b = √(2)a cm.
b is the diagonal of the inscribed square.
c²+a² = (4+6)²
c = √(100-a²) cm.
d = c-a
d = (√(100-a²)-a) cm.
14...
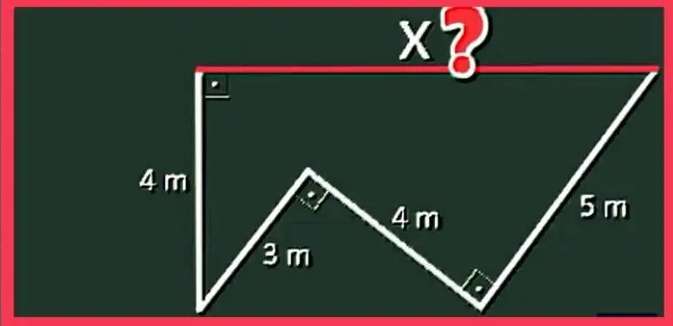
a = (4-b) m.
Calculating b.
3 - 5
b - (4-b)
Cross Multiply.
3(4-b) = 5b
12-3b = 5b
8b = 12
b = 1.5 m.
Recall.
a = (4-b)
And b = 1.5 m.
a= 4-1.5
a= 2.5 m.
c = √(3²+1.5²)+...