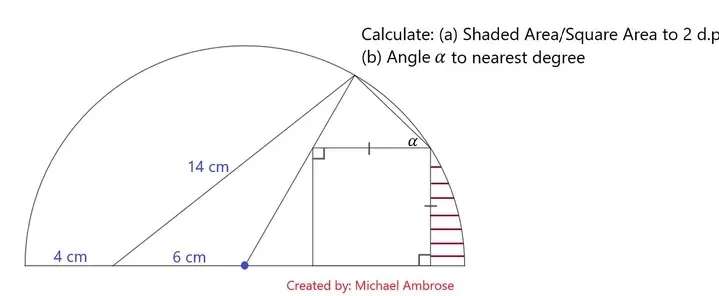
Mathematics Question and Solution
Let the side length of the inscribed square be a.
b² = 2a²
b = √(2)a cm.
b is the diagonal of the inscribed square.
c²+a² = (4+6)²
c = √(100-a²) cm.
d = c-a
d = (√(100-a²)-a) cm.
14² = 6²+(4+6)²-2*6*10cose
196 = 136-120cose
120cose = -60
e = acos(-½)
e = 120°
f = 180-e
f = 60°
Calculating a.
tan60 = a/(√(100-a²)-a)
√(3)(√(100-a²)-a) = a
√(3(100-a²))-√(3)a = a
√(300-3a²) = a+√(3)a
300-3a² = a²+2√(3)a²+3a²
300 = 7a²+2√(3)a²
(7+2√(3))a² = 300
a² = 28.6694463637 cm²
a² is the area of the inscribed square.
It implies;
a = √(28.6694463637)
a = 5.354385713 cm.
Again, a is the side length of the inscribed square.
Recall.
c = √(100-a²)
Again a² = 28.6694463637 cm²
c = √(100-28.6694463637)
c = 8.4457417458 cm.
tang = 5.354385713/8.4457417458
g = 32.373659127°
Therefore, shaded area is;
Area sector with radius 10 cm and angle 32.373659127° - Area triangle with height 5.354385713 cm and base 8.4457417458 cm respectively.
(32.373659127π*100/360)-(0.5*5.354385713*8.4457417458)
= 28.2513471342-22.6108794697
= 5.6404676645 cm²
(a) Shaded Area ÷ Square Area to 2 decimal places is;
5.6404676645÷28.6694463637
= 0.1967414227
≈ 0.2
(b) Calculating angle alpha to the nearest degree.
Let it be h.
sin60 = 5.354385713/j
j = 6.1827120655 cm.
k = 10-j
k = 3.8172879345 cm.
It implies;
l² = 3.8172879345²+5.354385713²-2*3.8172879345*5.354385713cos30
l = 4.7751336693 cm.
Therefore, angle alpha to the nearest degree (h) is;
(4.7751336693/sin60) = (3.8172879345/sinh)
h = 43.8131704367°
h ≈ 44°