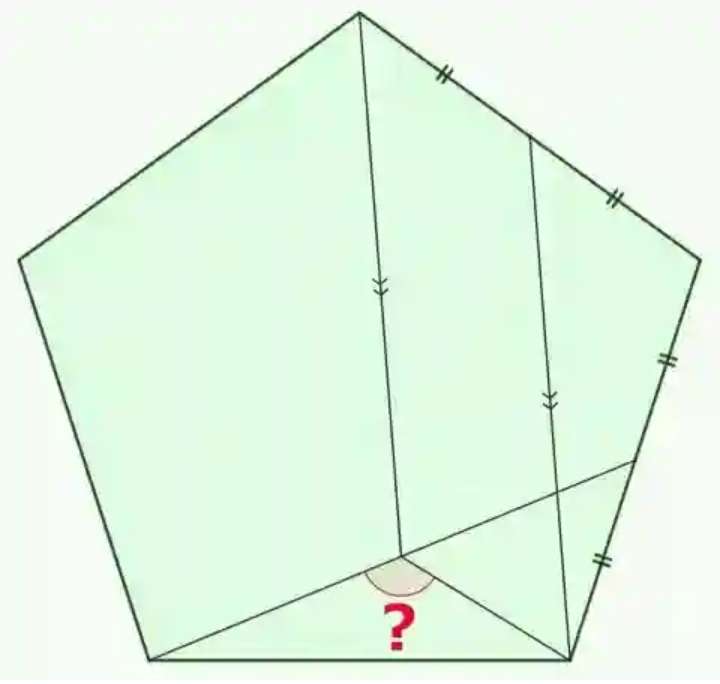
Mathematics Question and Solution
Let the side length of the ascribed regular pentagon be 2 units.
a = ⅕*180(5-2)
a = 108°
a is the single interior angle of the ascribed regular pentagon.
b² = 2²+1²-2*1*2cos108
b = 2.497212041 units.
(2.497212041/sin108) = (1/sinc)
c = 22.3861775592°
d = 180-108-c
d = 49.6138224408°
e = 180-d
e = 130.3861775592°
f = d-c
f = 27.2276448816°
g = 180-2d
g = 80.7723551184°
h = 180-g-f
h = 72°
(2.497212041/sin72) = (j/sin27.2276448816)
j = 1.2013397144 units.
k² = 1.2013397144²+1²-2*1.2013397144*1cos49.6138224408
k = 0.9415063562 units.
(0.9415063562/sin49.6138224408) = (1/sinl)
l = 54°
Therefore, ?, the required angle is;
Let it be m.
m+l = 180
m+54 = 180
m = 180-54
m = 126°
Again, m is the required angle.