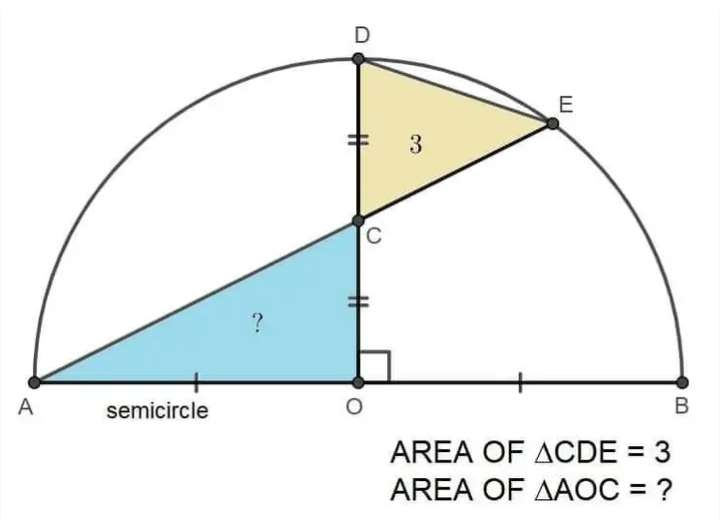
Mathematics Question and Solution
Let a be the radius of the ascribed half circle.
tanb = a/(0.5a)
b = atan(2)°
b is angle OCA = angle DCE.
c = atan(½)°
c is angle OAC.
d² = a²+(½(a))²
d = √(¼(5a²))
d = ½√(5)a² units.
d = 1.1180339887a units.
d is AC.
cos(atan(½)) = e/(2a)
e = 1.788854382a units.
e is AE.
f = e-d
f = 0.6708203933a units.
f is CE.
Calculating a.
0.5*0.6708203933a*0.5asin(atan(2)) = 3
0.3a² = 6
3a² = 60
a² = 20
a = √(20)
a = 2√(5) units.
Again, a is the radius of the ascribed half circle.
g = ½(a)
g = √(5) units.
g is OC = CD.
Therefore, area triangle AOC (area inscribed blue triangle) is;
½(ag)
= ½*2√(5)*√(5)
= √(5)²
= 5 square units.