Sir Mike Ambrose is the author of the question.
Area R exactly in its simplest decimal form is;
Area triangle with height 4.54406194214 units and base 2sin(atan(2)) units.
= ½*4.54406194214*...

Let the radius of the inscribed circle be r.
The square side is 8 cm.
b = 8-r
c = 2+r
Therefore;
(2+r)² = 2²+(8-r)²
4+4r+r² = 4+64-16r+r²
4r = 64-16r
20r = 64
5r = 16
r = (16/5)...

Sir Mike Ambrose is the author of the question.
Let length AB = 2 units.
Therefore;
Side length of the square, x is;
2x² = 2²
x = √(2) units.
It implies;
Area square is;
x²...

Sir Mike Ambrose is the author of the question.
Inscribed square single side length is;
7.80540954246 cm
Area green in cm² to 1 decimal place is;
Area trapezoid with parallel sides 12 cm...

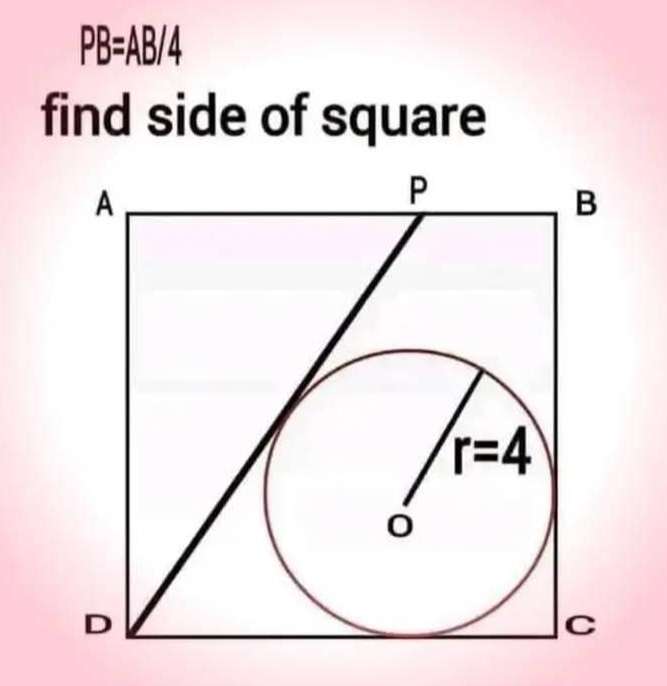
Sir Mike Ambrose is the author of the question.
Let the side let of the square be 2 units.
Therefore;
Area square is;
2²
= 4 square units.
It implies;
Area R is;
Area trapezoi...
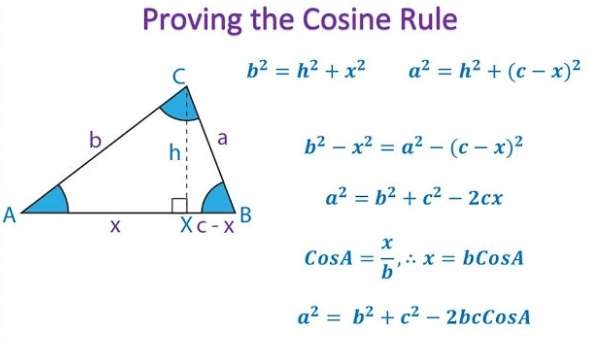
Area blue is;
Area triangle with height 10 cm and base (10sin16.26025509) cm - Area semi circle with radius √(2) cm
= (0.5*10*10sin16.26025509) - (½π√(2)²)
= (14-π) cm²
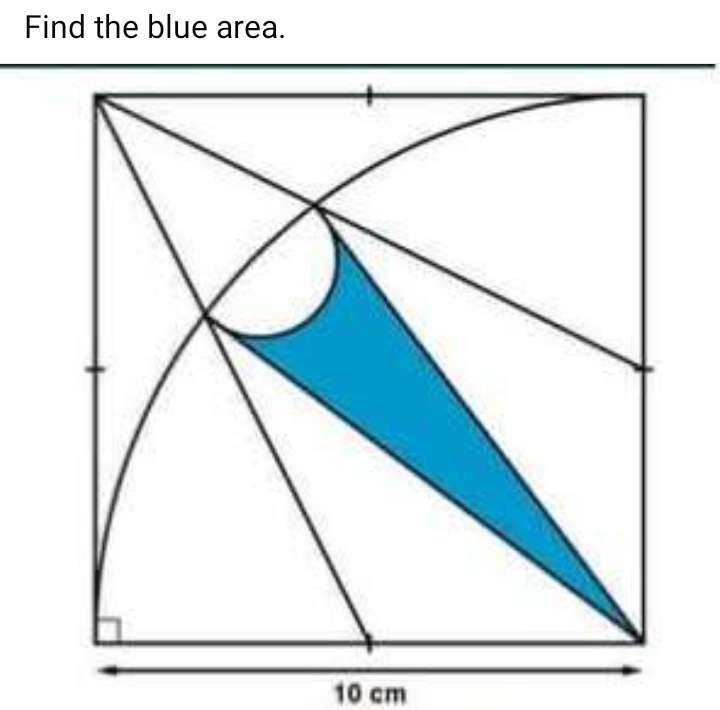
Let AB = x
PB = x/4
Therefore;
a = x - (x/4)
a = (3x/4) units.
b² = x²+(3x/4)²
b = √(x²+(3x/4)²) units.
c = (x-4) units.
It implies that;
½(x*(3x/4)) + ½(4*√(x²+(3x/4)²)) + ½(4...
Sir Mike Ambrose is the author of the question.
Let the single side length of the square be 2 unit.
Therefore;
Area square is;
2²
= 4 square units
It implies;
Area R is;
Area...
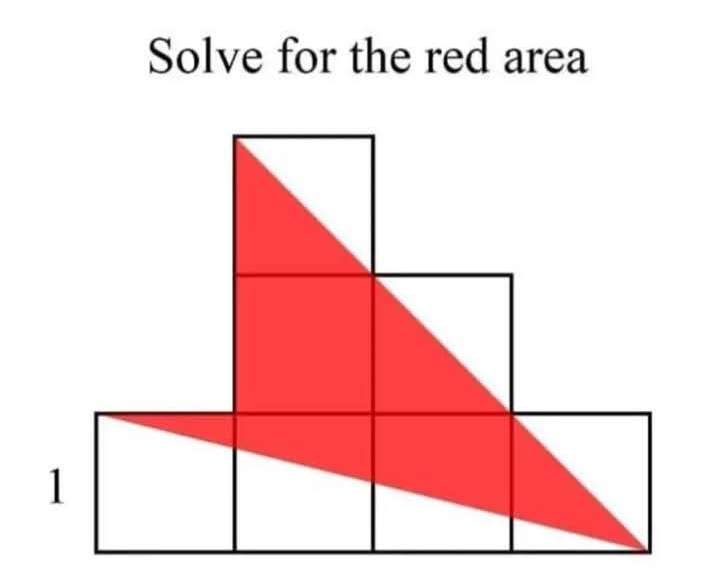
Red Area is;
7(area square with side 1 unit) - Area triangle with base 1 unit and height 4 units - Area square with side 1 unit - Area triangle with height and base 1 unit respectively.
= 7(1...