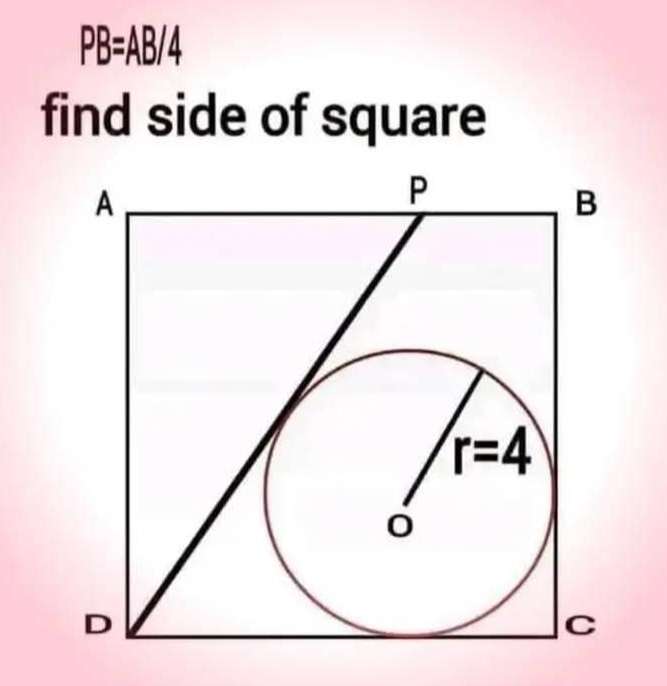
Mathematics Question and Solution
Let AB = x
PB = x/4
Therefore;
a = x - (x/4)
a = (3x/4) units.
b² = x²+(3x/4)²
b = √(x²+(3x/4)²) units.
c = (x-4) units.
It implies that;
½(x*(3x/4)) + ½(4*√(x²+(3x/4)²)) + ½(4*(x-4)) + (4*4) + ½((x/4)+4)*(x-4) = x²
⅛(3x²) + 2√(x²+(3x/4)²) + 2(x-4) + 16 + ½(¼(x+16))(x-4) = x²
2√(x²+(3x/4)²) + 2x + 8 + ⅛(x²+12x-64) = ⅛(5x²)
16√(x²+(3x/4)²)+16x+64+x²+12x-64 = 5x²
16√(x²+(3x/4)²)+28x = 4x²
Dividing through by 4
4√(x²+(3x/4)²)+7x = x²
16(x²+(9x²/16)) = x⁴-14x³+49x²
16(25x²/16) = x⁴-14x³+49x²
25x² = x⁴-14x³+49x²
Dividing through by x²
25 = x²-14x+49
x²-14x+24 = 0
x²-12x-2x+24 = 0
x(x-12)-2(x-12) = 0
(x-12)(x-2) = 0
x ≠ 2
x = 12 units.
Where x is the side of the square.