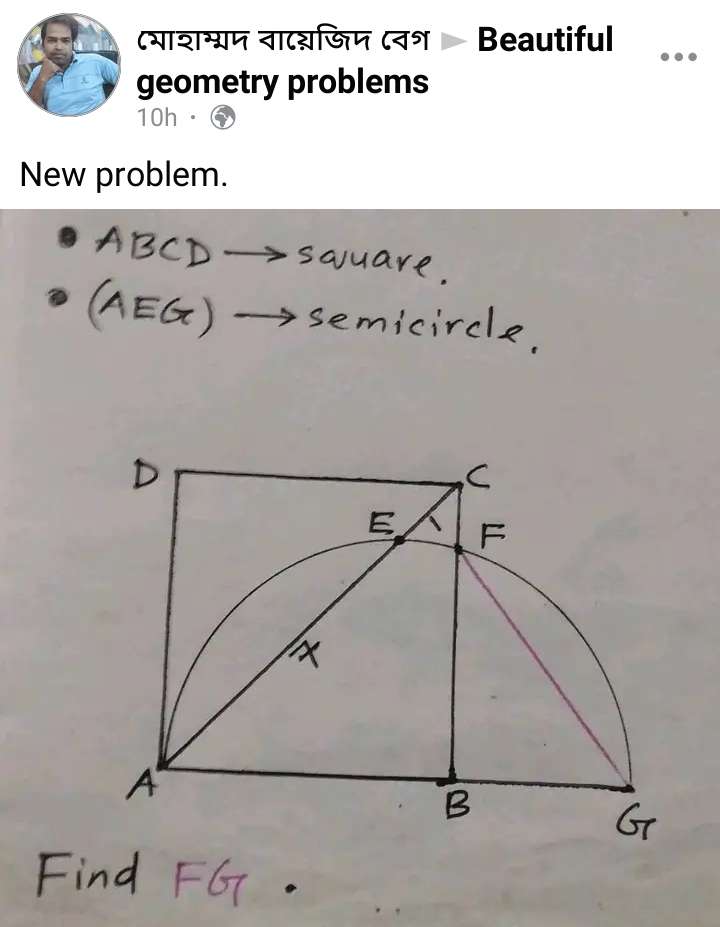
Mathematics Question and Solution
Calculating the side length of square ABCD.
2x² = 8²
x² = 32
x = 4√(2) units.
Where x is AB.
Let BG = y
Semi circle radius r is;
r = ½(4√(2)+y) units.
Calculating y.
sin45 = ½(4√(2)+y)/7
½(√(2)) = (4√(2)+y)/14
√(2) = (4√(2)+y)/7
y = 7√(2)-4√(2)
y = BG = 3√(2) units.
Calculating r.
r = ½(4√(2)+y)
And y = 3√(2) units.
r = ½(4√(2)+3√(2))
r = ½(7√(2)) units.
a = x-r
a = 4√(2)-½(7√(2))
a = ½√(2) units.
Calculating BF.
(BF)² = r²-a²
(BF)² = (½(7√(2)))²-(½√(2))²
(BF)² = ½(49)-½
(BF)² = ½(48)
(BF)² = 24
BF = 2√(6) units.
It implies;
Length FG (red length) is;
√((BF)²+(BG)²)
= √((2√(6))²+(3√(2))²)
= √(24+18)
= √(42) units.