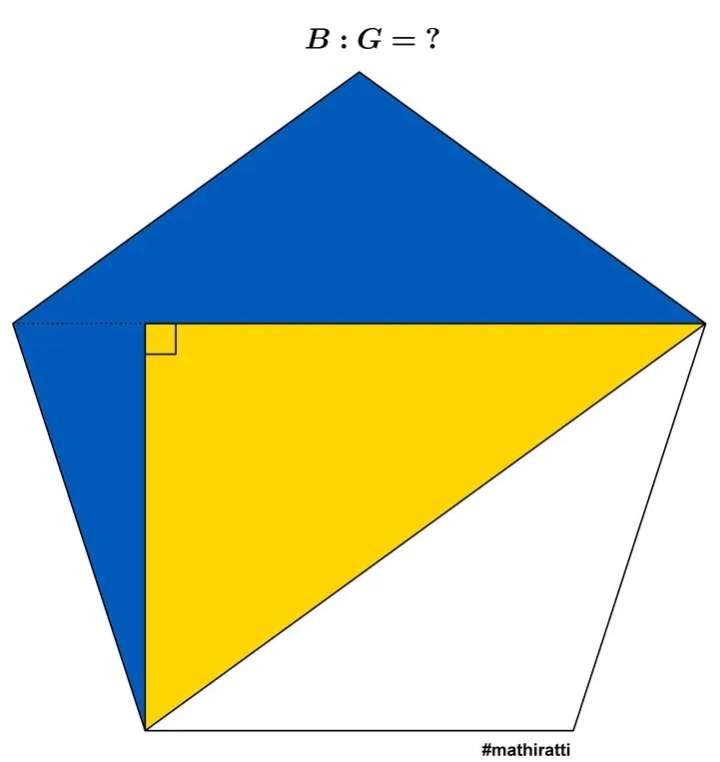
Let the side length of the regular pentagon be 1 unit.
a² = 2-2cos108
108° is the single interior angle of the regular pentagon.
a = 1.6180339887 units.
sin72 = b/1
b = 0.9510565163 units.
cos72...
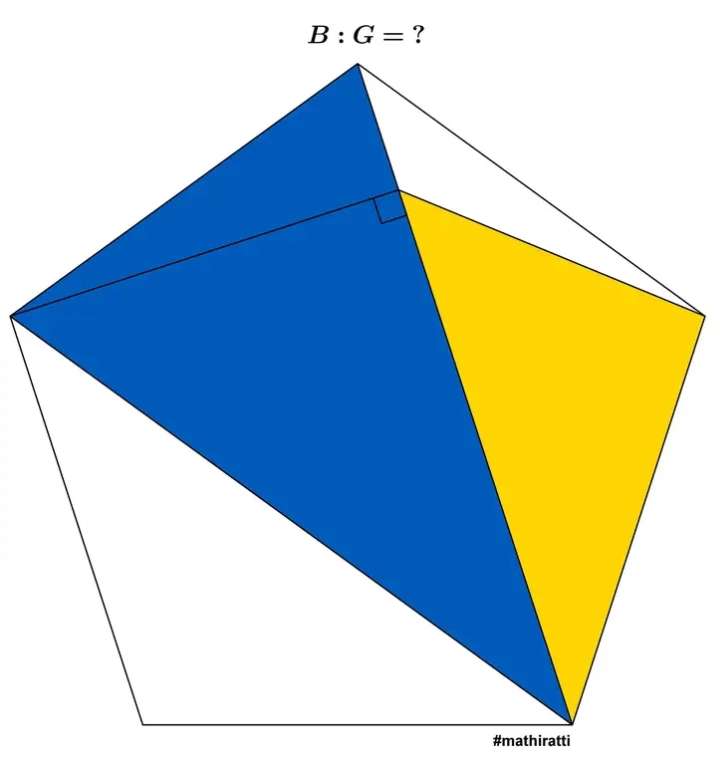
Let the side length of the regular pentagon be 1 unit.
a² = 2-2cos108
108° is the single interior angle of the regular pentagon.
a = 1.6180339887 units.
Area Blue is;
0.5*1*1.6180339887s...
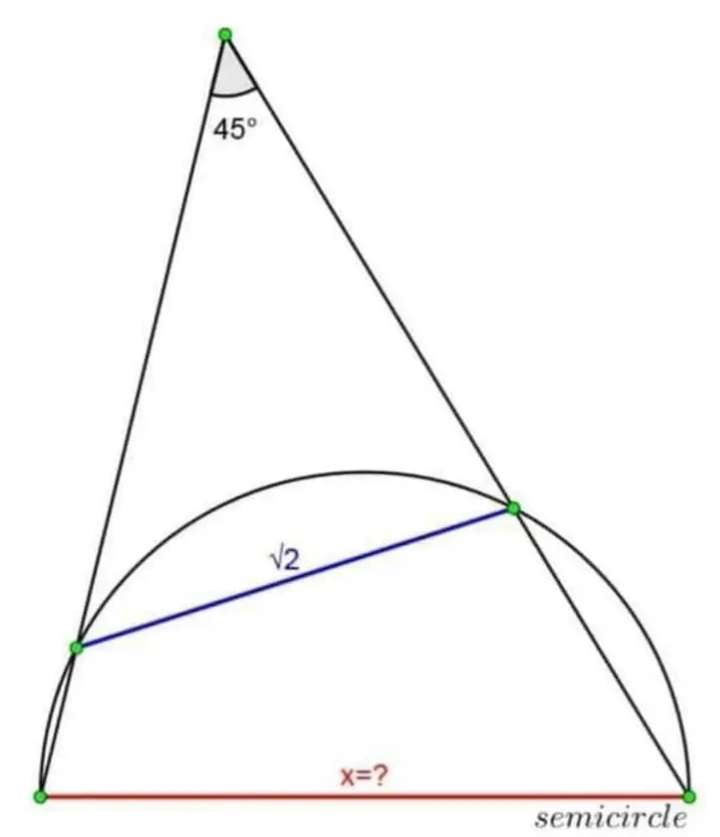
It implies;
2a² = √(2)²
Where a is the radius of the half circle.
Therefore;
2a² = 2
a² = 1
a = 1 unit.
Again, a is the radius of the half circle.
x (diameter of the half circle) is;...
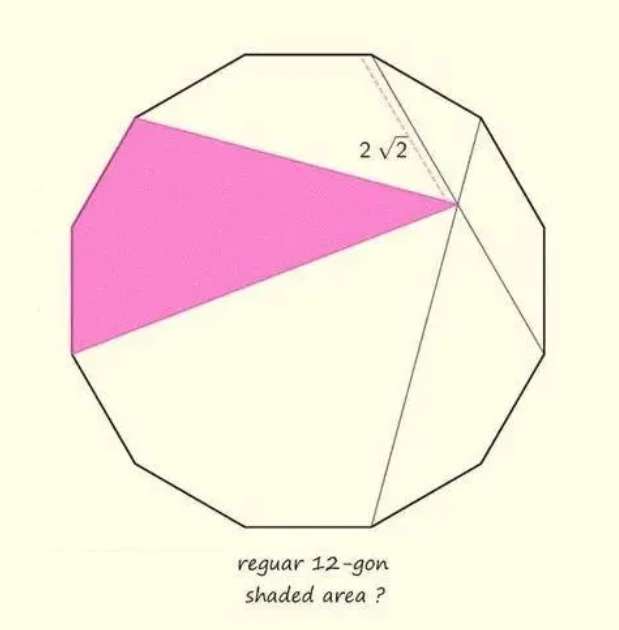
b = (180(12-2))/12
b = 1800/12
b = 150°
b is the single interior angle of the regular dodecagon.
2c+2(150) = 360
2c = 60
c = 30°
d = 150-15-30
d = 105°
2e+3(150) = 180(5-2)
2e = 540-450
2e = 90
e...

Let the inscribed square side be 1 unit.
sin30 = a/1
a = ½ units.
a = 0.5 units.
a is the side length of one of the four congruent isosceles inscribed shaded triangle.
sin60 = b/1
b = ½√(3) units....
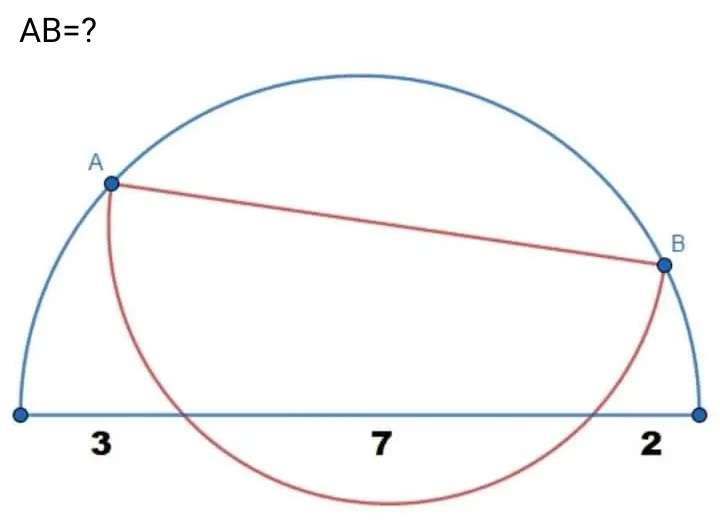
Let a be half AB.
b = ½(3+7+2)
b = 6 units.
It implies;
6² = a²+c²
c² = 36-a²
c = √(36-a²) units.
d = ½(7)
d = 3.5 units.
e = 4-3.5
e = 0.5 units.
Therefore;
c² = 0.5²+f²...
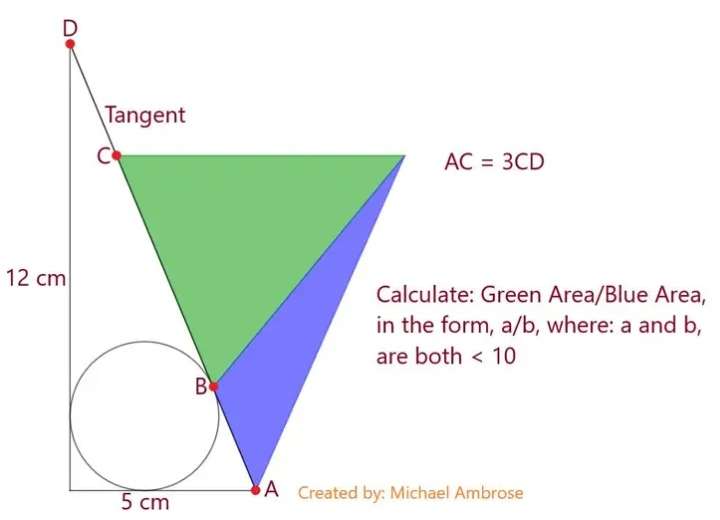
a² = 12²+5²
a = √(144+25)
a = 13 cm.
a is AD.
12b+5b+13b = 12*5
30b = 60
b = 2 cm.
b is the radius of the inscribed circle.
tanc = 12/5
c = atan(12/5)°
tan(0.5c) = 2/d
⅔ = 2/d
d =...
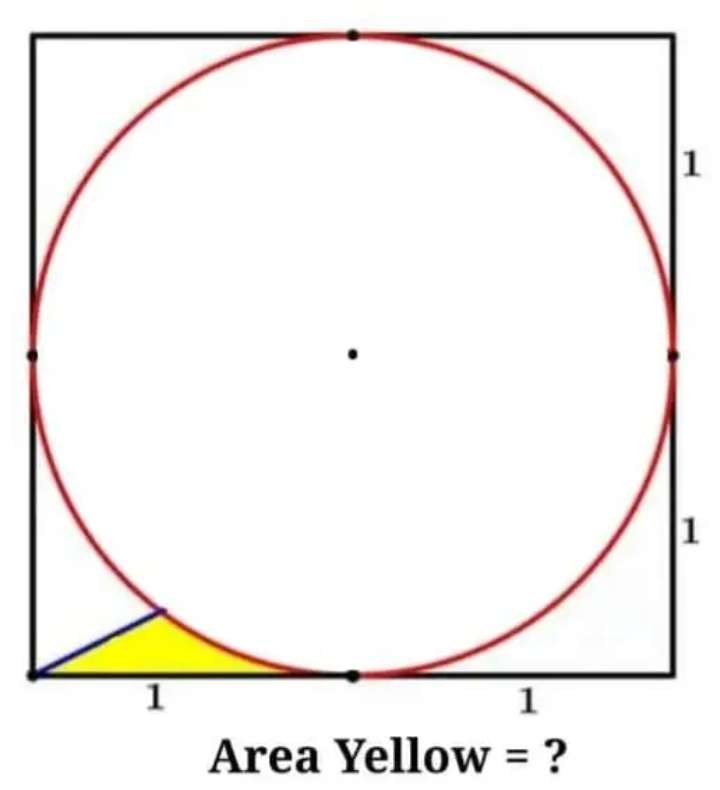
tana = 1/2
a = atan(1/2)°
b = 180-2a
b = (180-2atan(½))°
Notice!
Radius of the inscribed circle is 1 unit.
Area yellow is;
Area triangle with height 2 units and base 1 unit - Area sq...

Calculating the area of the inscribed square.
a = ½(45)
a = 22.5°
b = ½(180-45)
b = ½(135)
b = 67.5°
cos22.5 = 6/c
c = 6.4943532018 units.
Let d be the side length of the inscribed...
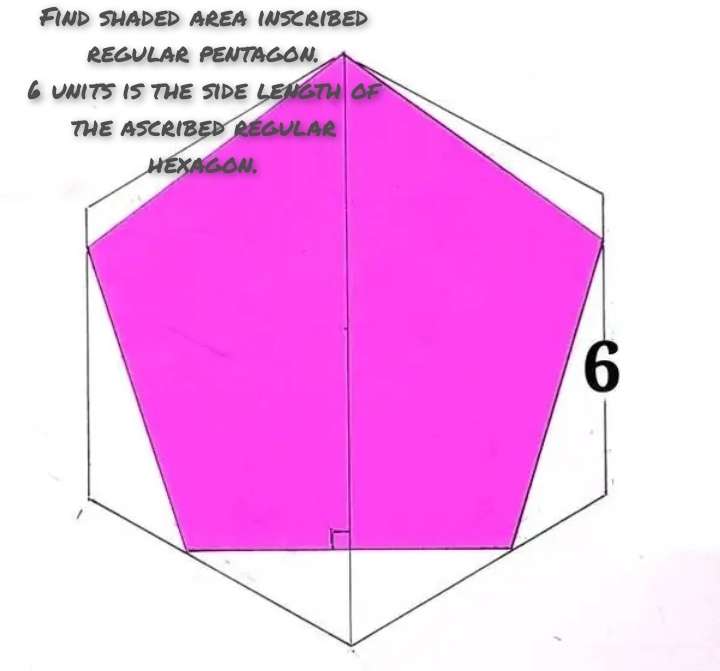
sin30 = a/6
a = 3 units.
b = 6+2a
b = 12 units.
Let the side length of the inscribed regular pentagon be c.
Calculating c.
d² = 2c²-2c²cos108
108° is the single interior angle of the...