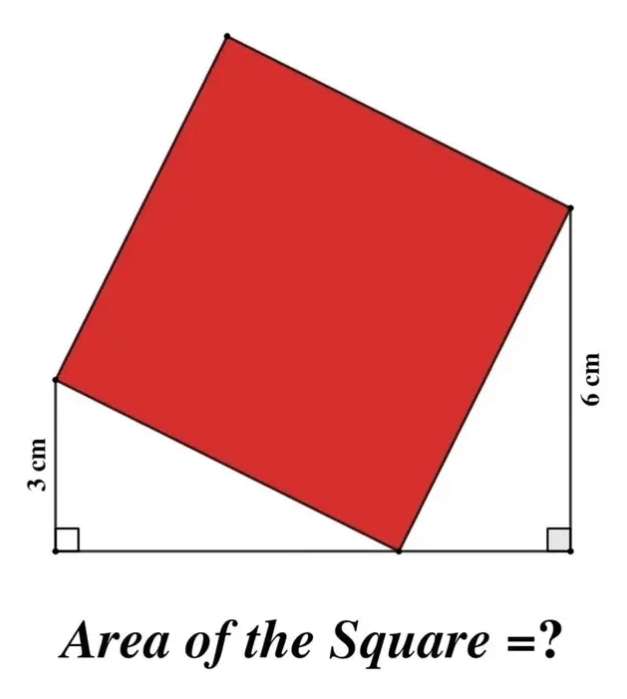
Let the side length of the red square be a units.
b²+3² = a²
b = √(a²-9) units.
c²+6² = a²
c = √(a²-36) units.
Observing similar plane shape (right-angled) side length ratios.
√(a²-9)...

Notice;
Diameter of the inscribed semi circle is ½ unit.
Therefore radius of the inscribed semi circle is ¼ unit.
Let the radius of the inscribed small circle be r.
Calculating r.
(1...
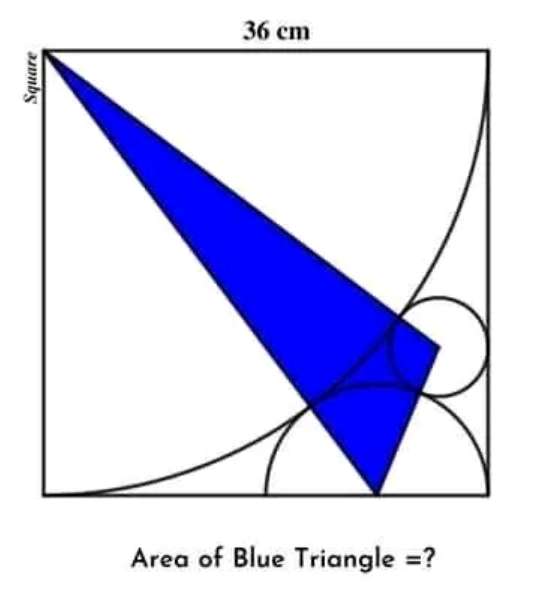
Radius of the inscribed quarter circle is 36 cm.
Radius of the inscribed semi circle is;
½(½(36))=9 cm.
Radius of the small inscribed circle is;
⅓(⅓(36))=4 cm.
Therefore the side lengths...
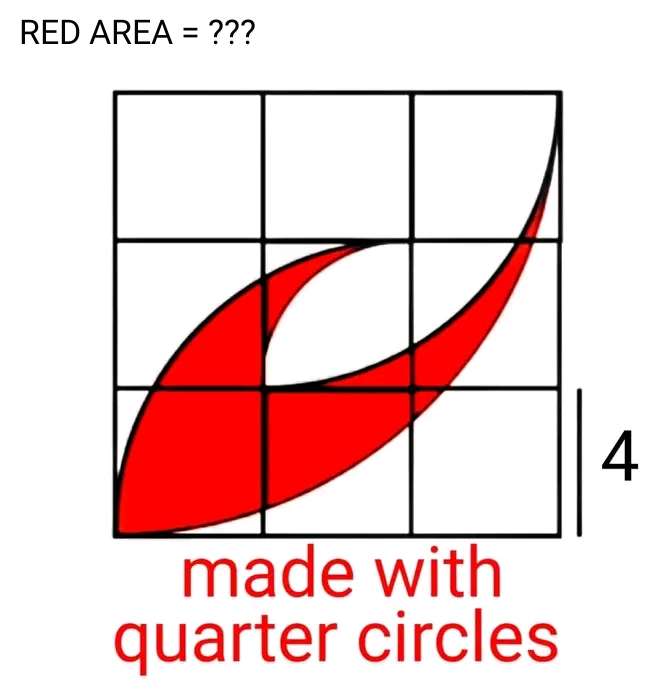
Notice!
The square side length is;
4+4+4
= 12 units.
Calculating Area Red.
Area quarter circle with radius 12 units - Area triangle with height and base 12 units respectively - Area quarte...
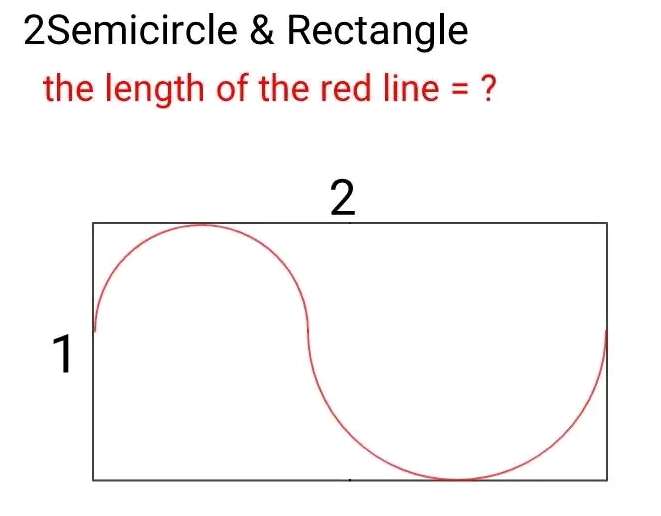
Let the diameter of the big inscribed half circle be a units.
It's radius is ½(a) units.
Let the diameter of the small inscribed half circle be b units.
It's radius is ½(b) units.
It im...
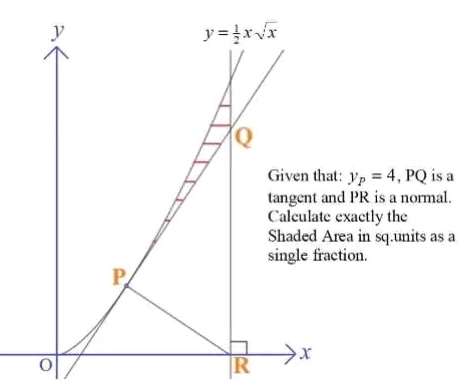
Equation of the curve is;
y = ½(x^(3/2))
It implies;
PR = √(4²+6²)
PR = 2√(13) units
QR = (2√(13))/(cos(90-atan(⅔)))
= 13 units.
Therefore;
Shaded Area is;
(Area under the cu...
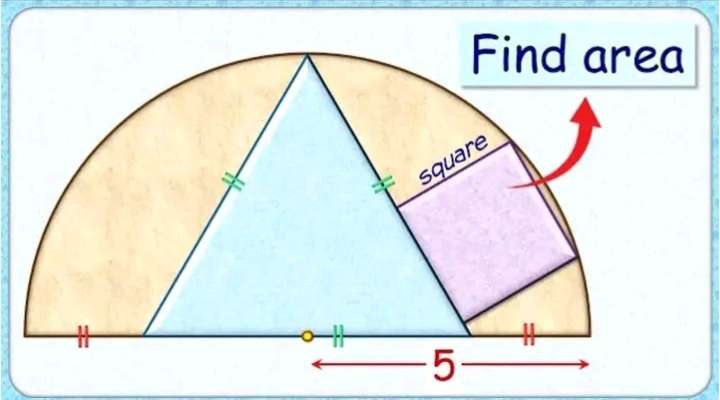
sin60 = 5/a
a = 5/(√(3)/2)
a = ⅓(10√(3)) units.
a is the side length of the inscribed regular triangle.
b = ½(a)
b = ⅓(5√(3)) units.
sin60 = c/⅓(5√(3))
√(3)/2 = 3c/(5√(3))
6c = 15
c =...
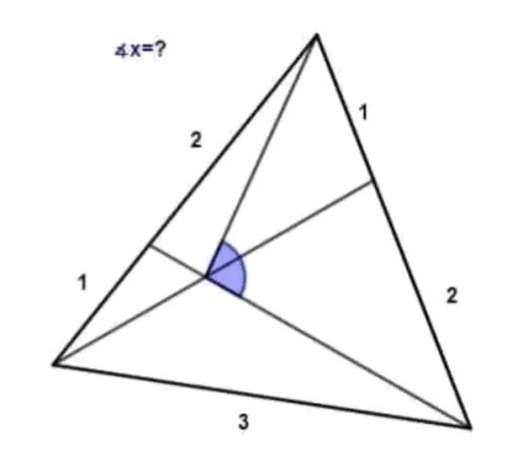
Notice!
The ascribed triangle is equilateral.
Calculating the required angle x.
a² = 1+3²-2*3cos60
a = √(7) units.
(√(7)/sin60) = (1/sinb)
b = 19.1066053509°
c = 60-b
c = 40.8933...
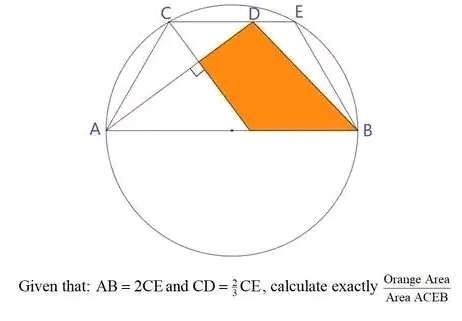
Let CE be 3 units.
Therefore:
Area Orange is;
Area triangle with height √(19) units and base 6sin(60-acos(4/√(19))) units - Area triangle with height (12√(19)/19) units and base (36√(57)/...
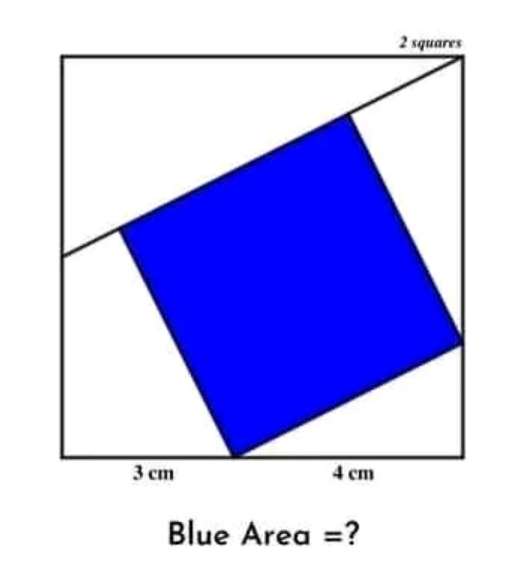
Let x be the single side length of the square.
Therefore;
x²=28-4√(x²-16) via similar triangle.
16(x²-16)=(28-x²)²
16x²-256=784-56x²+x⁴
x⁴-72x²+1040=0
Let x²(blue area) = P
Therefore;
P...