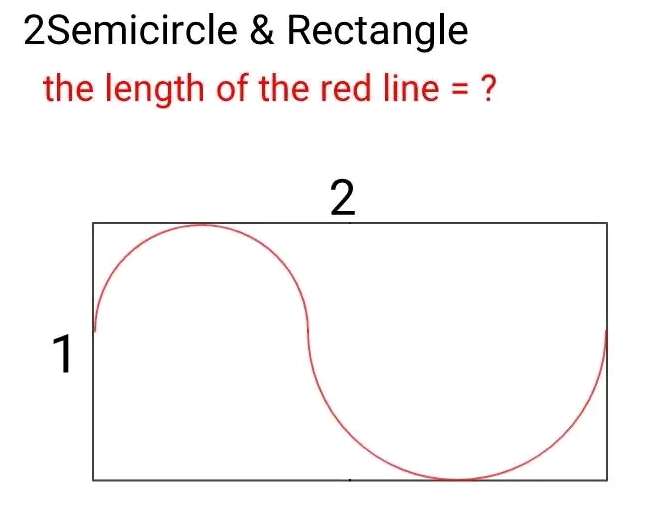
Mathematics Question and Solution
Let the diameter of the big inscribed half circle be a units.
It's radius is ½(a) units.
Let the diameter of the small inscribed half circle be b units.
It's radius is ½(b) units.
It implies;
a+b = 2 --- (1).
c = ½-½(b)
c = ½(1-b) units.
d = (a-½) units.
Equation c and d.
c = d
½(1-b) = a-½
a = 1+½(b) --- (2).
Substituting (2) in (1).
a+b = 2
And a = 1+½(b)
1+½(b)+b = 2
½(b)+b = 1
1.5b = 1
½(3b) = 1
3b = 2
b = ⅔ units.
Again, b is the diameter of the small inscribed half circle.
Radius, r of small inscribed half circle is;
r = ½(b)
r = ½*⅔
r = ⅓ units.
Calculating a.
Using (2).
a = 1+½(b)
And b = ⅔ units.
a = 1+½*⅔
a = 1+⅓
a = 1⅓ units.
a = (4/3) units.
Again, a is the diameter of the small inscribed half circle.
Radius, R of small inscribed half circle is;
R = ½(a)
R = ½*(4/3)
R = ⅔ units.
Therefore length red is;
The summation of the circumference of two half circles with radius ⅓ units and ⅔ units respectively.
= (½*2π*⅓)+(½*2π*⅔)
= ⅓π+⅔π
= π units.