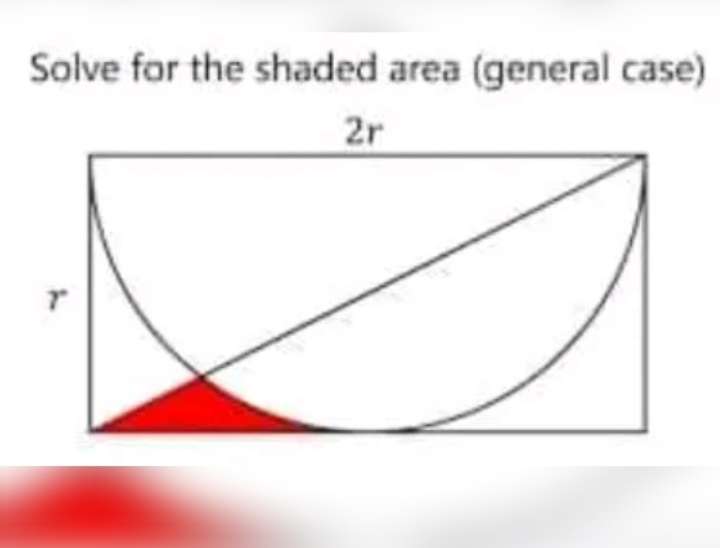
Red area is;
½(Area rectangle of length 2r and width r - area semi circle of radius r) - area triangle of height 2r and base r + area sector of radius r and angle (2tan–¹(1/2))° + area triangle...
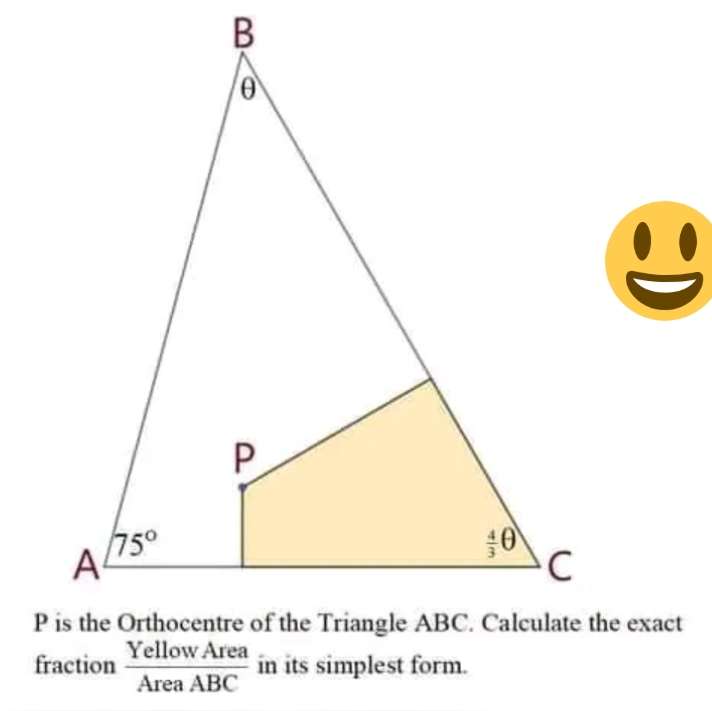
Sir Mike Ambrose is the author of the question.
Please, move the question left or right to review the solution.
Thank you!
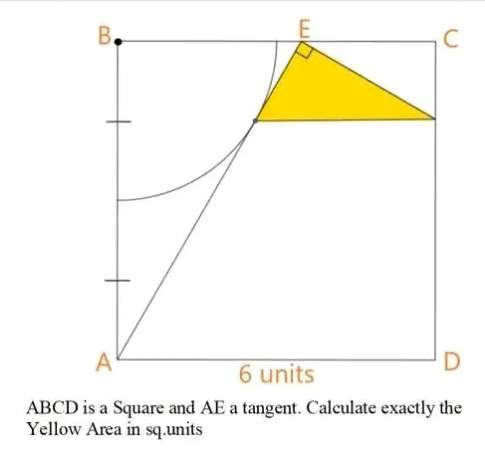
Sir Mike Ambrose is the author of the question.
Yellow Area exactly in square units is;
½*√(3)*(4√(3)-4)
= ½(12-4√(3))
= 2(3-√(3)) square units.
= 2.5358983849 square units.
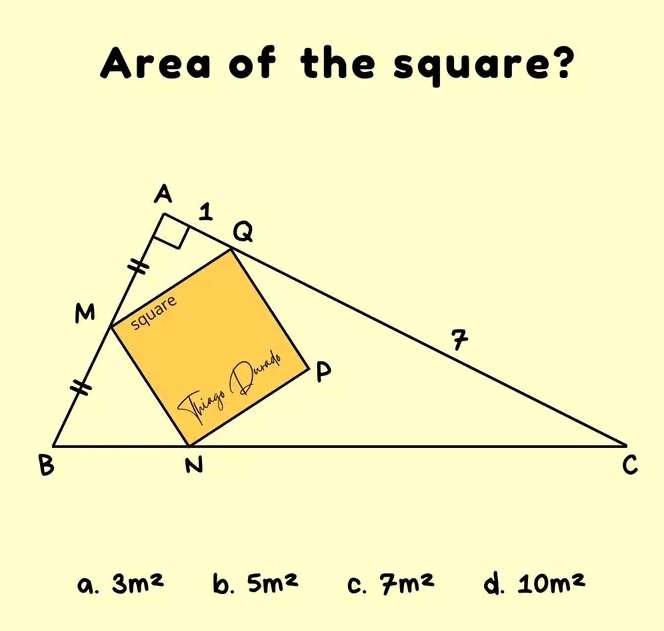
Let the inscribed square side length be a.
b²+1² = a²
b = √(a²-1) units.
c = 2b
c = 2√(a²-1) units
d = 1+7
d = 8 units.
Observing similar plane shape (right-angled) side length rati...

Mazana Job Shared The Questions.
Number 1.
a = 180-30-45
a = 105°
It implies;
(4/sin105) = (b/sin30)
b = 2.0705523608 units.
c = 45+90
c = 135°
Therefore, the required length,...
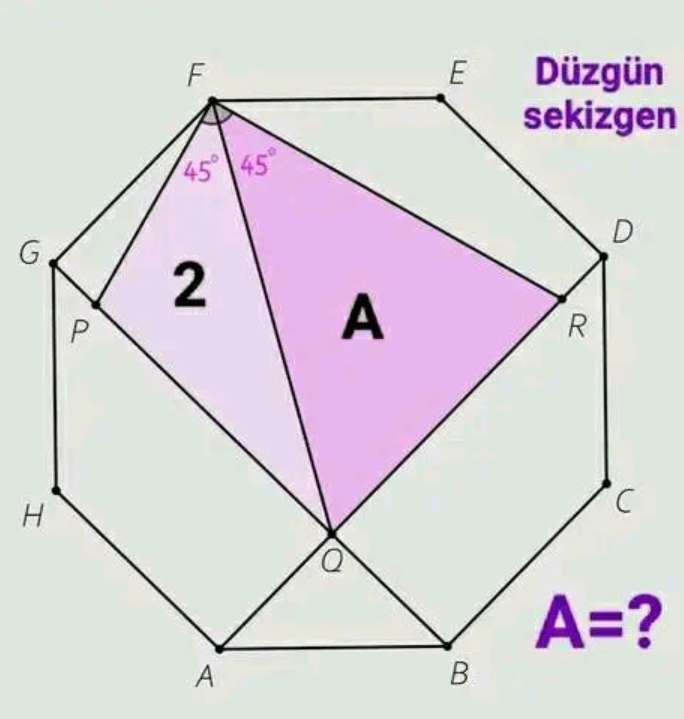
Let the side length of the regular octagon be a.
b = ⅛*180(8-2)
b = 135°
b is the single interior angle of the regular octagon.
2c² = a²
c = √(a²/2)
c = ½(√(2)a) units.
c = 0.7071067812a...
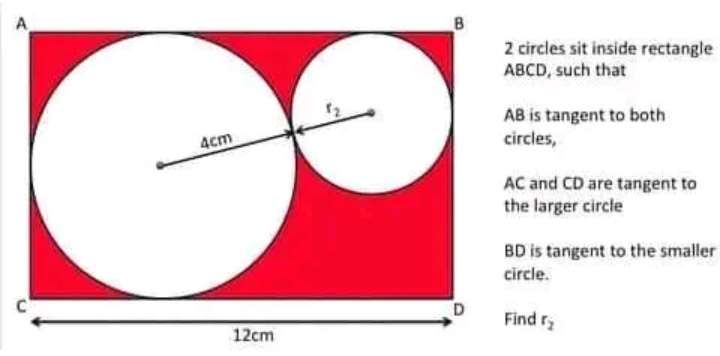
r2 will be;
Let it be x.
Therefore;
(4+x)²=(8-x)²+(4-x)²
16+8x+x²=64-16x+x²+16-8x+x²
x²-32x+64=0
(x-16)²=-64+256
x = 16±8√(3)
x ≠ 16+8√(3)
x = 16-8√(3)
Therefore;
x = r2 = 8(2-√...
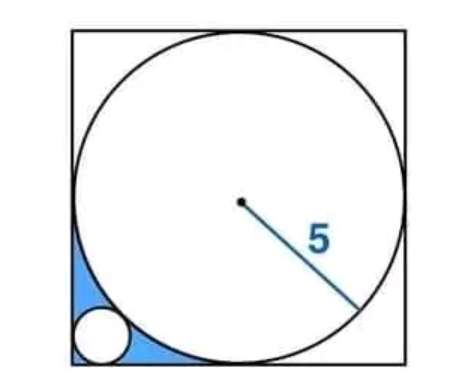
The radius, r if the small circle will be;
(5+r)²=2(5-r)²
25+10r+r²=50-20r+2r²
Therefore
r²-30r+25=0
(r-15)²=-25+225
r = 15±√(200)
r = 15±10√(2)
It implies;
r ≠ 15+10√(2)
r = 15...
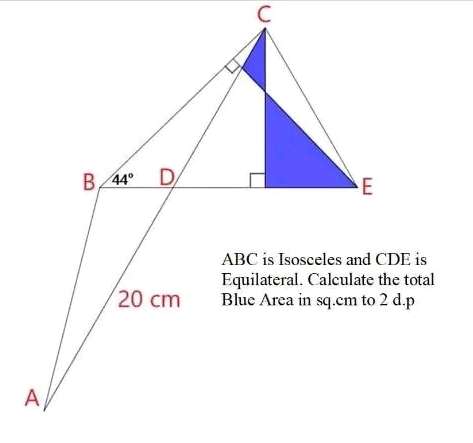
Sir Mike Ambrose is the author of the question.
Notice!
AB = BC
Calculating AB.
AB = (20sin60)/sin104
AB = BC = 17.85075169007 cm.
Calculating BD
BD = (20sin16)/sin104
BD = 5.6815...
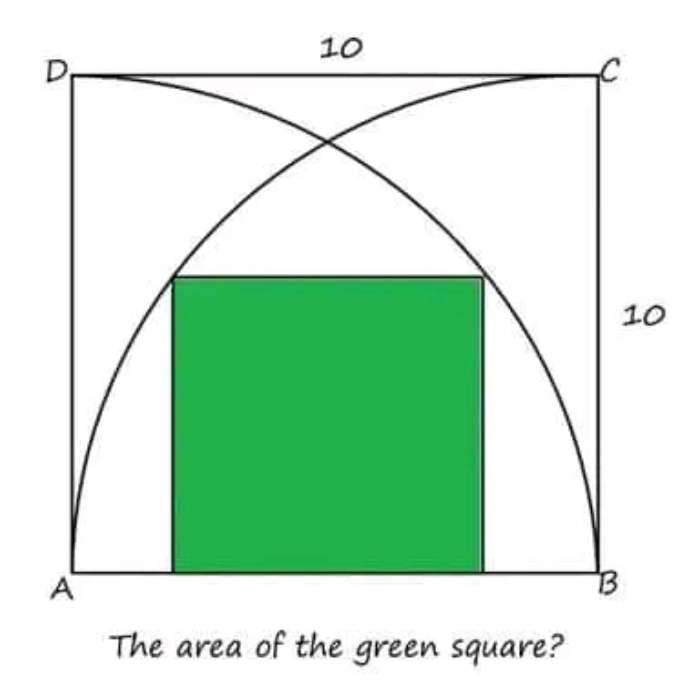
Let the side length of the inscribed green square be a.
b = ½(10-a) units.
c = b+a
c = ½(10-a+2a)
c = ½(10+a) units.
Therefore, a² (area green inscribed triangle) is;
10² = a²+(½(10+a...