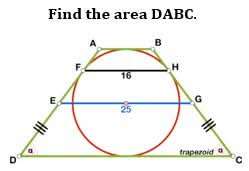
Mathematics Question and Solution
Calculating area ABCD.
Let x be the radius of the inscribed circle.
a = ½(16)
a = 8 units.
x² = 8²+a²
a = √(x²-64) units.
b = ½(25) units.
It implies;
x ~ 8
½(25) ~ x
Cross Multiply.
x² = 100
x = 10 units.
Again, x is the radius of the inscribed circle.
c = 2x
c = 20 units.
c is the diameter of the inscribed circle, and also, the height of the isosceles trapezoid.
sind = 10/(0.5*25)
d = asin(20/25)
d = asin(4/5)°
tan(asin(4/5)) = 20/f
f = 15 units.
g = x-√(10²-(0.5*16)²)
g = 10-√(100-64)
g = 4 units.
tan(asin(4/5)) = 4/h
h = 3 units.
j = 16-2h
j = 16-2(3)
j = 10 units.
j is AB.
k = 2f+j
k = 2(15)+10
k = 40 units.
k is CD.
It implies;
Area ABCD, an isosceles trapezoid is;
½(AB+CD)*c
= ½(10+40)*20
= ½(1000)
= 500 square units.