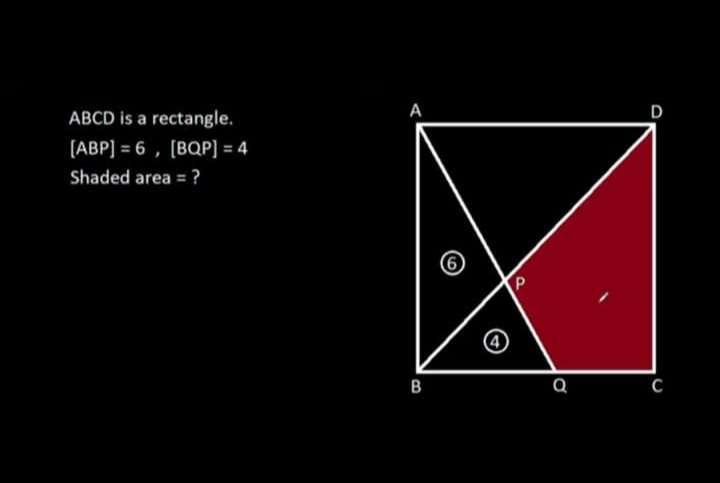
Mathematics Question and Solution
Calculating Red Area.
Let AB = CD = x.
Let AD = BC = y.
½*xa = 10
a = 20/x units.
a is BQ.
½*xb = 6
b = 12/x units.
b is the horizontal height of area 6 (area triangle APB).
c = y-b
c = y-(12/x)
c = (xy-12)/x units.
c is the horizontal height of triangle CPD (red area).
d = y-a
d = y-(20/x)
d = (xy-20)/x units.
d is CQ.
½*e*(20/x) = 4
10e = 4x
e = ⅖(x) units.
e is the vertical height of area 4 (area triangle BPQ).
Therefore;
Calculating Area Rectangle ABCD (xy).
½*x*(xy-12)/x+½*(xy-20)/x*⅖(x) = ½*xy-4
½(xy)-6+⅖(½(xy)-10) = ½(xy)-4
⅖(½(xy)-10) = 6-4
⅕(xy)-4 = 2
⅕(xy) = 6
xy = 30 square units.
Again, xy is the area of rectangle ABCD.
Therefore;
½(xy) is the area of triangle BCD.
It implies;
Red Area (area CDPQ) is;
½(xy)-(Area triangle BPQ)
= ½(30)-4
= 15-4
= 11 square units.