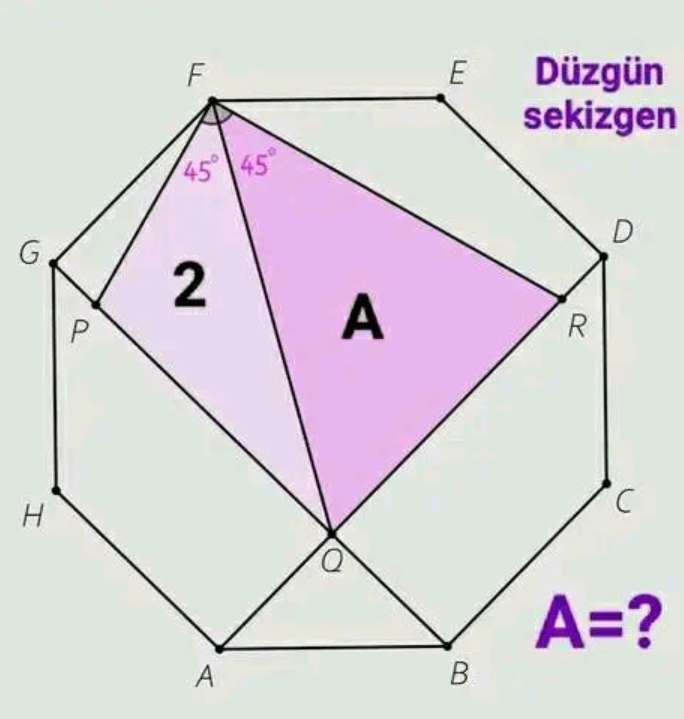
Mathematics Question and Solution
Let the side length of the regular octagon be a.
b = ⅛*180(8-2)
b = 135°
b is the single interior angle of the regular octagon.
2c² = a²
c = √(a²/2)
c = ½(√(2)a) units.
c = 0.7071067812a units.
c is AQ = BQ
d = a+c
d = 1.7071067812a units.
d is GQ.
tane = 1.7071067812a/a
e = 59.6388065954°
e is angle GFQ.
f = e-45
f = 14.6388065954°
f is angle GFP.
g = 180-(90-f)
g = 104.6388065954°
g is angle FPQ.
h = 90-e
h = 30.3611934046°
h is angle FQG.
cos14.6388065954 = a/j
j = 1.0335509007a units.
j is FP.
tan14.6388065954 = k/a
k = 0.261203875a units.
k is GP.
l = d-k
l = 1.7071067812a-0.261203875a
l = 1.4459029062a units.
l is PQ.
Calculating a, side length of the regular octagon.
0.5*1.4459029062a*1.0335509007a(sin104.6388065954) = 2
0.7229514531a² = 2
a² = 2.7664374854
a = 1.6632610996 units.
Again, a is the side length of the regular octagon.
sin30.3611934046 = 1.6632610996/m
m = 3.2906575521 units.
m is FQ.
n = 180-45-59.6388065954
n = 75.3611934046°
n is angle FRQ.
(3.2906575521/sin75.3611934046) = (o/sin45)
o = 2.4049140577 units.
o is QR.
It implies;
Area A (area triangle FQR) is;
0.5*3.2906575521*2.4049140577sin59.6388065954
= 3.4142135625 square units.
= (2+√(2)) square units.