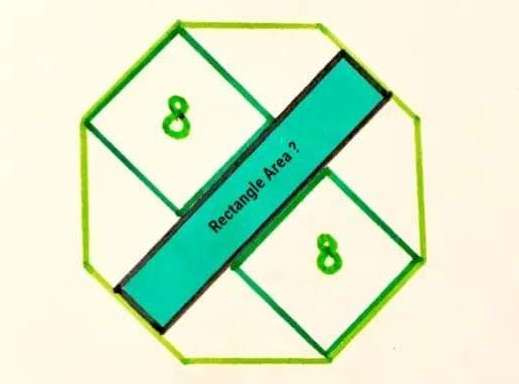
Mathematics Question and Solution
Let the side of the regular octagon be a.
Calculating a.
a² = 8
a = √(8)
a = 2√(2) units.
2b² = (2√(2))²
b = 2 units.
c = 2√(2)+2+2
c = (2√(2)+4) units.
Where c is the length of the inscribed rectangle.
d = c-2(2√(2))
d = (2√(2)+4)-4√(2)
d = (4-2√(2)) units.
Where d is the width of the inscribed rectangle.
Area Rectangle is;
cd
= (2√(2)+4)*(4-2√(2))
= 8 square units.