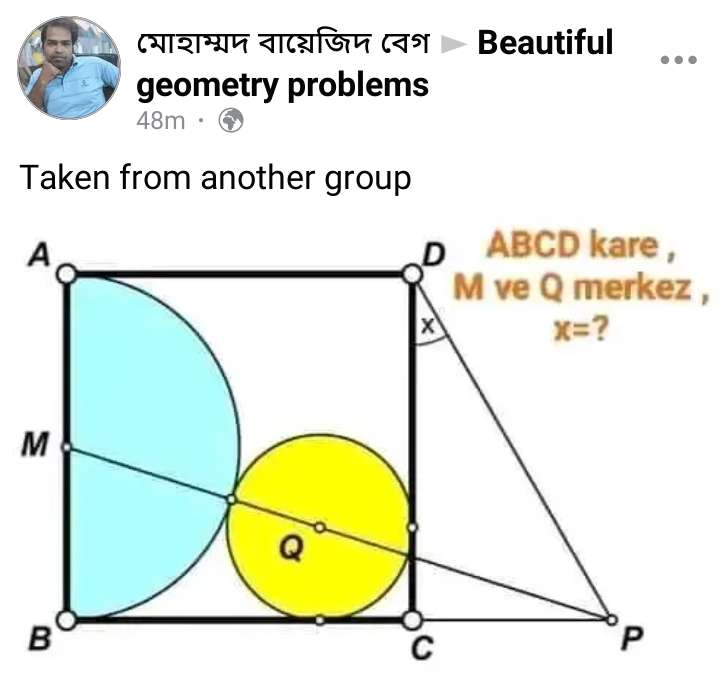
Mathematics Question and Solution
Let the AB be 4 cm.
Therefore, radius of the inscribed semi circle is;
radius = 2 cm.
Let the radius of the inscribed circle be r.
Calculating r.
(2+r)² = (4-r)²+(2-r)²
4+4r+r² = 16-8r+r²+4-4r+r²
4+4r+r² = 20-12r+2r²
r²-16r+16r = 0
(r-8)²+16-(-8)² = 0
(r-8)² = 64-16
(r-8)² = 48
r = 8±4√(3)
It implies;
r ≠ (8+4√(3)) cm.
r = (8-4√(3)) cm.
Therefore;
MQ = 2+r
MQ = 2+(8-4√(3))
MQ = (10-4√(3)) cm.
a = 2-r
a = 2-(8-4√(3))
a = (4√(3)-6) cm
b = acos(a/MQ)
b = acos((4√(3)-6))/(10-4√(3)))
b = 72.41204622601°
tan72.41204622601 = BP/BM
tan72.41204622601 = BP/2
BP = 6.30940107676 cm.
It implies;
CP = BP-BC
CP = 6.30940107676-4
CP = 2.30940107676 cm.
Therefore x° (angle CDP) is;
atan(2.30940107676/4)
= 30.00000000002°
= 30°