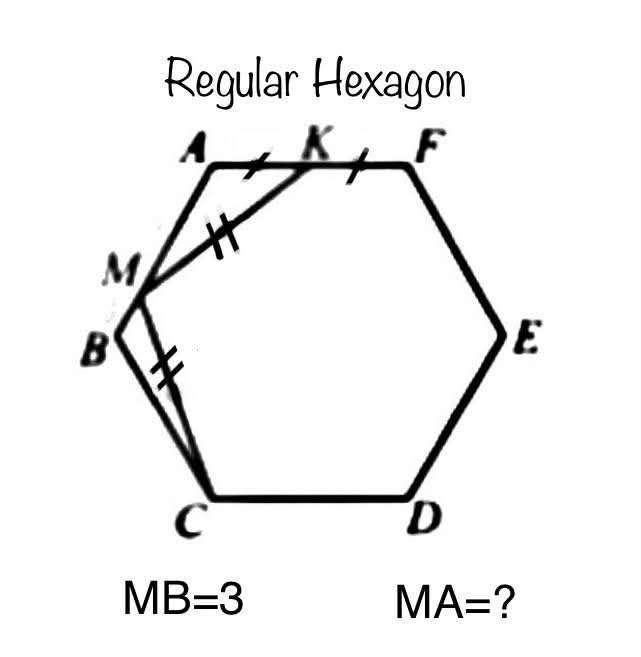
Mathematics Question and Solution
Calculating Length MA.
Let a be the AB, side length of the regular hexagon.
b = (a-3) units.
b is AM.
c = ½(a) units.
c is AK = FK.
Let d be CM = KM.
It implies;
d² = a²+3²-2*3acos120
d² = a²+9+3a --- (1).
Again.
d² = (0.5a)²+(a-3)²-2*½(a)(a-3)cos120
d² = ¼(a²)+a²-6a+9+½(a²-3a)
d² = ¼(a²+4a²-24a+36+2a²-6a)
d² = ¼(7a²-30a+36) --- (2).
Equating (1) and (2).
a²+9+3a = ¼(7a²-30a+36)
4a²+12a+36 = 7a²-30a+36
42a = 3a²
a = ⅓(42)
a = 14 units.
Again a is AB, the side length of the regular hexagon.
It implies;
MA = AB-MB
MA = 14-3
MA = 11 units.