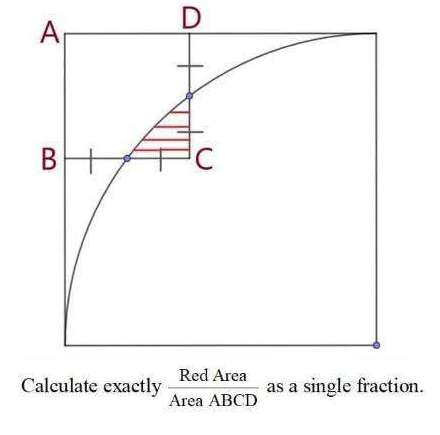
Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
Let AB be 2 units.
Area ABCD is;
2²
= 4 square units.
Let the side length of the ascribed square be x.
Calculating x.
a = (x-2) units.
b = (x-1) units.
It implies;
x² = a²+b²
x² = (x-2)²+(x-1)²
x² = x²-4x+4+x²-2x+1
x²-6x+5 = 0
Therefore;
x = 5 units.
Again, x is the side length of the ascribed square.
c = x-2
c = 3 units.
d = x-1
d = 4 units.
tane = 3/4
e = atan(3/4)°
f = 90-2e
f = 90-2atan(3/4)
f = (atan(4/3)-atan(3/4))°
f = 16.2602047083°
Calculating shaded area.
It is;
Area isosceles right-angled triangle with side length 1 units + Area sector with side length 5 units and angle (atan(4/3)-atan(3/4))° - Area isosceles triangle with side 5 units and angle (atan(4/3)-atan(3/4))°
= ½(1*1)+((atan(4/3)-atan(3/4))*5*5π÷360)-½(5*5sin(atan(4/3)-atan(3/4)))
= ½+((atan(4/3)-atan(3/4))*5*5π÷360)-½(7)
= ((atan(4/3)-atan(3/4))*5*5π÷360)-3
= (5(90-2atan(3/4))π)÷72)-3
= ((5(90-2atan(3/4))π)-216)/72 square units.
= 0.5474263651 square units.
Therefore;
Red shaded area ÷ Area ABCD exactly is;
(((5(90-2atan(3/4))π)-216)/72)÷4
= ((5(90-2atan(3/4))π)-216)/288
Exactly in decimal is;
0.5474263651÷4
= 0.13685659128