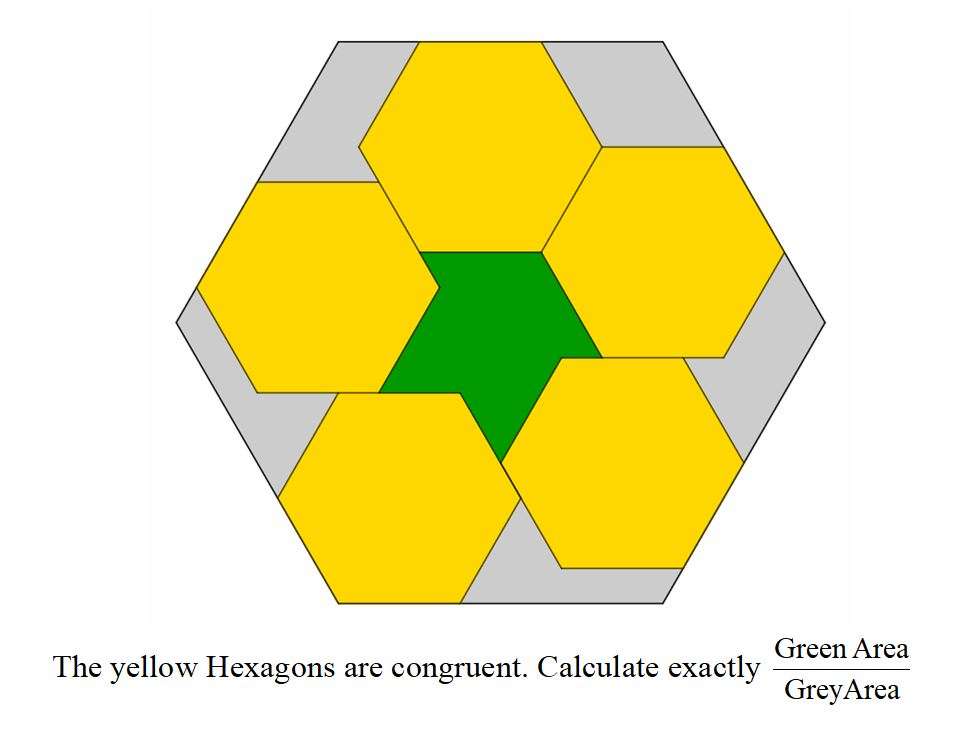
Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
Let the side length of the five inscribed congruent regular hexagon be 1 unit.
It implies;
The ascribed regular hexagon is;
2+(⅔)
= ⅓(8) units.
Area Green is;
2(area triangle with height ⅓ unit and base ⅓(sin60) units) + 2(area parallelogram with height ⅓√(3) unit and base ⅓(4) units)
= 2(½*⅓*⅓*sin60) + 2(⅓*√(3)*⅓*4)
= (√(3)/18) + (8√(3)/9)
= (17√(3)/18) square units.
Area Grey is;
Area regular hexagon with side (8/3) units - 5(area regular hexagon with side 1 unit) - Area Green.
= (½(6*(8/3))*(8/(2*3tan(180/6)))) - 5((½*6)*(1/2tan(180/6))) - (17√(3)/18)
⅓(32√(3)) - ½(15√(3)) - (17√(3)/18)
= 20√(3)/9 square units.
It implies;
Area Green ÷ Area Grey exactly is;
(17√(3)/18) ÷ (20√(3)/9)
= 17/40