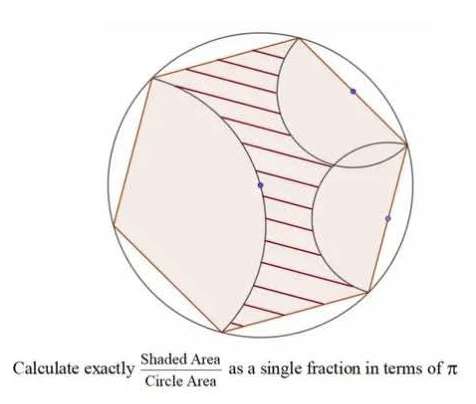
Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
Let the ascribed circle's radius be 1 unit.
Area ascribed circle is;
π(1)²
= π square units.
Calculating shaded area.
Notice.
The side length of the inscribed regular heptagon is equal the radius of the circle, 1 unit.
Therefore, shaded area is;
6(area equilateral triangle with side length 1 unit)-Area sector with radius 1 unit and angle 120°-2(area sector with radius 0.5 units and angle 120°)-2(area equilateral triangle with side length 0.5 units).
= 6(½*1*1*sin120)-⅓(1*1*π)-2(⅓*½*½*π)-2(½*½*½*sin60)
= ½(3√(3))-⅓(π)-⅙(π)-(√(3)/8)
= ⅛(11√(3))-½(π)
= ⅛(11√(3)-4π) square units.
It implies;
Shaded Area ÷ Area Circle is;
⅛(11√(3)-4π)÷π
= (11√(3)-4π)/(8π) Exactly in fraction.
= 0.5953924651 in decimal.