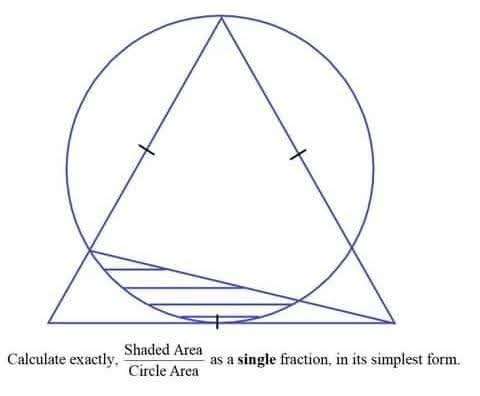
Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
Let the side length of the introduced equilateral triangle inscribing the circle be 2 units.
Calculating r, radius of the circle.
cos30 = 1/r
r = 1/cos30
r = 2/√(3)
r = ⅓(2√(3)) units.
Area circle is;
πr²
= π(⅓(2√(3)))²
= ⅓(4π) square units.
= 4.18879020479 square units.
tan30 = a/1
a = ⅓√(3) units.
b = r-a
b = ⅓(2√(3))-⅓√(3)
b = ⅓√(3) units.
tan60 = ⅓√(3)/c
c = ⅓ units.
cos60 = (⅓)/d
d = ⅔ units.
or
sin60 = ⅓√(3)/d
½√(3) = ⅓√(3)/d
½ = (⅓)/d
d = ⅔ units.
f = 2+2c
f = 2+⅔
f = ⅓(8) units.
g = 2+c
g = ⅓(7) units.
h² = (√(3)/3)²+(⅓(7))²
h² = ⅓+⅑(49)
h² = 52/9
h = √(52/9)
h = ⅔√(13) units.
(⅔√(13)/sin60) = (⅔/sinj)
(2√(13)/3)÷(√(3)/2) = (2/3sinj)
(2√(13)/√(3) = 1/sinj
sinj = √(3)/(2√(13))
j = 13.897886248°
k = (120-asin(√(3)/(2√(13))))°
l = 180-k
l = 180-(120-asin(√(3)/(2√(13))))°
l = (60+asin(√(3)/(2√(13))))°
m = l-30
m = (30+asin(√(3)/(2√(13))))°
m = 43.897886248°
n = 180-2m
n = 92.204227504°
It implies;
Area sector with radius ⅓(2√(3)) units and angle 92.204227504° - Area with height ⅓(2√(3)) units and base ⅓(2√(3))sin(92.204227504) units.
= (92.204227504π(⅓(2√(3)))²÷360)-(0.5*(⅓(2√(3)))²sin92.204227504)
= 1.0728449028-0.66617338753
= 0.40667151527 square units.
Therefore,
Shaded Area ÷ Circle Area exactly in decimal is;
0.40667151527÷4.18879020479
= 0.0970856728
≈ 0.1 to 2 decimal places.