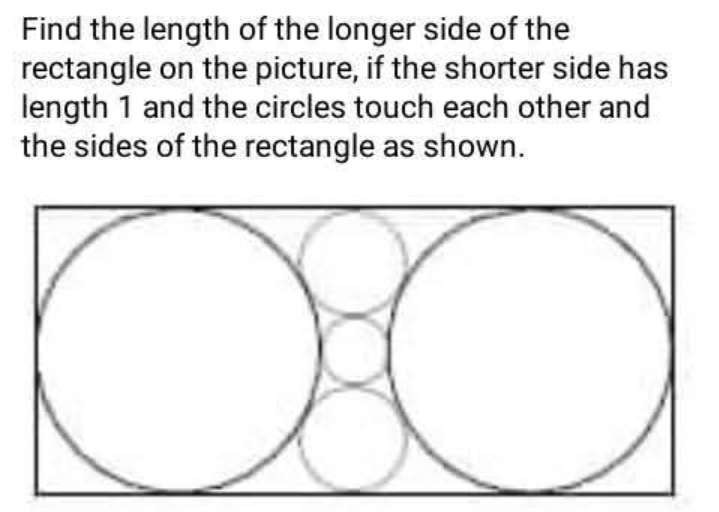
Mathematics Question and Solution
Let the two equal smaller inscribed circle radius be r.
Let the radius of the smallest inscribed circle be q.
The radius is the biggest inscribed circle is 0.5 units.
Therefore;
x+2r=0.5
r=½(0.5-x) ----- (1)
(0.5+r)²=(0.5+x)²+(x+r)²
0.25+r+r²=0.25+x+x²+x²+2xr+r²
r=x+2x²+2xr
r(1-2x)=x+2x²
r=(x+2x²)/(1-2x) ------- (2)
Equating (1) and (2).
(x+2x²)/(1-2x)=½(0.5-x)
4x²+2x=(0.5-x)(1-2x)
4x²+2x=0.5-x-x+2x²
2x²+4x-0.5=0
x²+2x-0.25=0
x²+x=0.25+1²
(x+1)²=0.25+1
x=-1±√(1.25)
x≠-1-√(1.25)
x=-1+√(1.25)
x=½(√(5))-1
The length of the rectangle is;
1+2(x)+1
And x=½(√(5))-1.
Therefore rectangle length will be;
1+2(½√(5)-1)+1
=2 + √(5) - 2
=√(5) units.