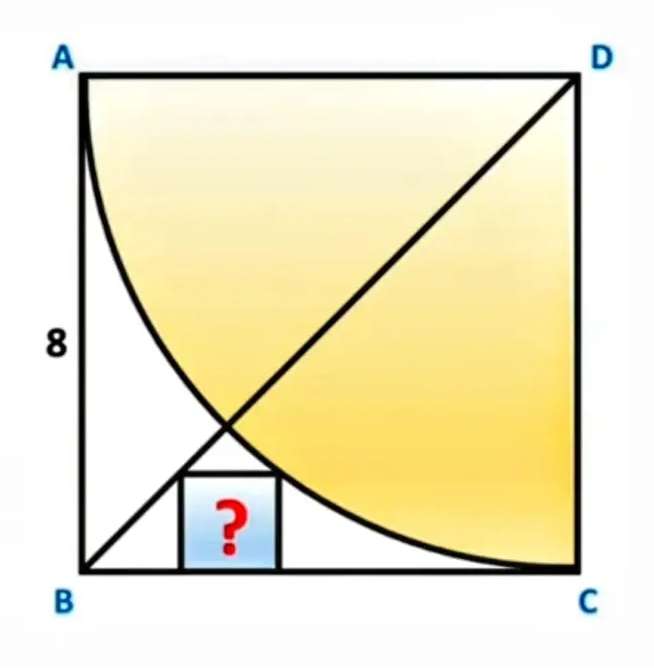
Mathematics Question and Solution
Calculating inscribed blue square area.
a² = 8²+8²
a = 8√(2) units.
b = a-8
b = (8√(2)-8) units.
Let c be the inscribed square side length.
d² = 2c²
d = √(2)c units.
e = a-d
e = (8√(2)-√(2)c) units.
Calculating c.
8² = c²+(8√(2)-√(2)c)²-2*c(8√(2)-√(2)c)cos45
64 = c²+128-32c+2c²-c(16-2c)
64 = c²+128-32c+2c²-16c+2c²
5c²-48c+64 = 0
Resolving the above quadratic equation via completing the square approach to get c, the side length of the inscribed square.
c²-⅕(48c) = -⅕(64)
(c-⅕(24))² = -⅕(64)+(-⅕(24))²
(c-⅕(24))² = -⅕(64)+(576/25)
(c-⅕(24))² = (576-320)/25
(c-⅕(24))² = (256/25)
c-⅕(24) = ±√(256/25)
c-⅕(24) = ±⅕(16)
c = ⅕(24)±⅕(16)
c = ⅕(24±16)
It implies;
c ≠ ⅕(40) ≠ 8 units.
c = ⅕(8) units.
Therefore, area blue inscribed square is;
c²
= (⅕(8))²
= (64/25) square units.
= 2.56 square units.