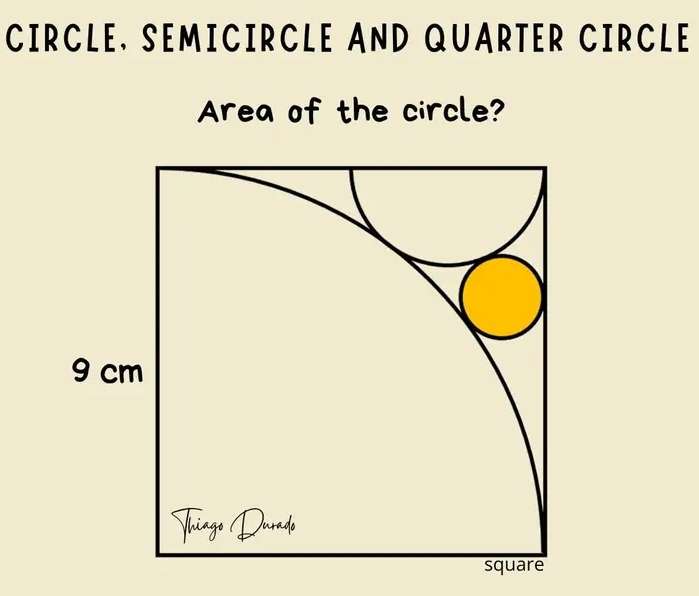
Mathematics Question and Solution
Let a be the radius of the inscribed semi circle.
Calculating a.
b² = 9²+9²
b² = 162
b = 9√(2) cm.
b is the diagonal of a square.
c = (9+a) cm.
It implies:
(9+a)² = a²+(9√(2))²-2*9√(2)acos45
(9+a)² = a²+162-18a
a²+18a+81 = a²+162-18a
36a = 81
4a = 9
a = ¼(9) cm.
Again, a is the radius of the inscribed semi circle.
Let d be the radius of the inscribed circle.
e = ((9/4)+d) cm.
f = ((9/4)-d) cm.
((9/4)+d)² = ((9/4)-d)²+g²
½(9)d+d² = d²-½(9)d+g²
9d = g²
g = 3√(d) cm.
h = 9-g
h = (9-3√(d)) cm.
j = (9+d) cm.
k = (9-d) cm.
Calculating d.
(9+d)² = (9-d)²+(9-3√(d))²
d²+18d = d²-18d+81-54√(d)+9d
36d = 81-54√(d)+9d
54√(d) = 81-27d
54²d = (81-27d)²
2916d² = 6561-4374d+729d²
2187d²+4374d-6561 = 0
½(81)d²+81d-½(243) = 0
81d²+162d-243 = 0
27d²+54d-81 = 0
3d²+6d-9 = 0
d²+2d-3 = 0
Resolving the above quadratic equation via factorization approach to get d, radius of the inscribed circle.
d²+3d-d-3 = 0
d(d+3)-1(d+3) = 0
(d+3)(d-1) = 0
It implies;
d ≠ -3
d = 1 cm.
Again, d is the radius of the inscribed circle.
Area inscribed circle is;
πd²
= π(1)²
= π cm²