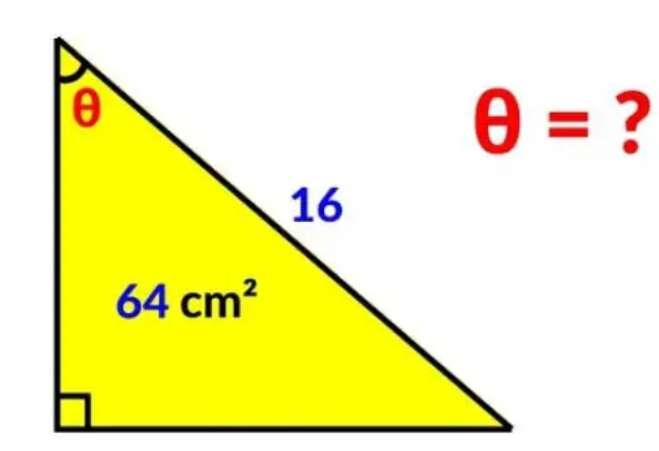
Mathematics Question and Solution
Let a and b be the height and base of the triangle respectively.
It implies;
½(ab) = 64
ab = 128 --- (1).
a²+b² = 16²
a = √(256-b²) --- (2).
Therefore, substituting (2) in (1) to get b.
ab = 128
And a = √(256-b²)
√(256-b²)b = 128
(256-b²)b² = (128)²
b⁴-256b²+16384 = 0
Let p = b²
It implies;
p²-256p+16384 = 0
Resolving the above quadratic equation via completing the square approach to get p.
(p-128)² = -16384+(-128)²
(p-128)²= 0
p = 128
And p = b²
b² = 128
b = √(128)
b = 8√(2) cm.
Recall.
ab = 128
And b = 8√(2) cm.
a = 128/b
a = 128/(8√(2))
a = 16/√(2)
a = 8√(2) cm.
It implies;
a = b
Meaning the triangle is an isosceles right-angled triangle.
Again, a and b are the height and base of the triangle respectively.
Therefore, the required angle, theta is;
Let it be c.
c = 45°