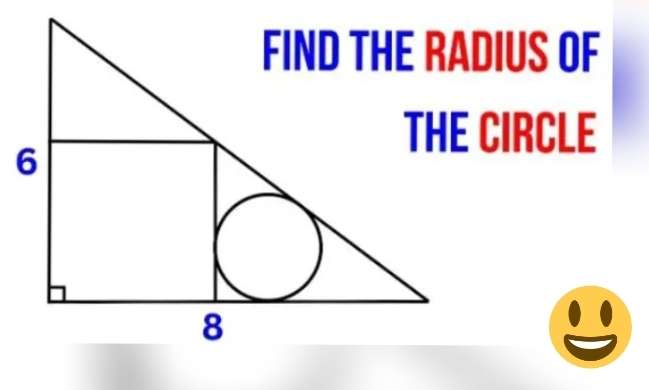
Mathematics Question and Solution
Let a be the side length of the inscribed square.
Calculating a.
b = (6-a) units.
Therefore;
6 - (6-a)
8 - a
Cross Multiply.
6a = 48-8a
14a = 48
7a = 24
a = (24/7) units.
Again, a is the side length of the inscribed square.
c = 8-a
c = 8-(24/7)
c = (32/7) units.
d² = 6²+8²
d = 10 units.
Recall.
b = (6-a) units.
And a = (24/7) units.
b = 6-(24/7)
b = (18/7) units.
e² = b²+a²
e² = (18/7)²+(24/7)²
e = √(900/49)
e = (30/7) units.
f = d-e
f = 10-(30/7)
f = (40/7) units.
Radius, r of the inscribed circle is;
fr+cr+ar = ac
(40/7)r+(32/7)r+(24/7)r = (24/7)(32/7)
(96/7)r = (768/49)
r = (768/49)÷(96/7)
r = ⅐(8) units.