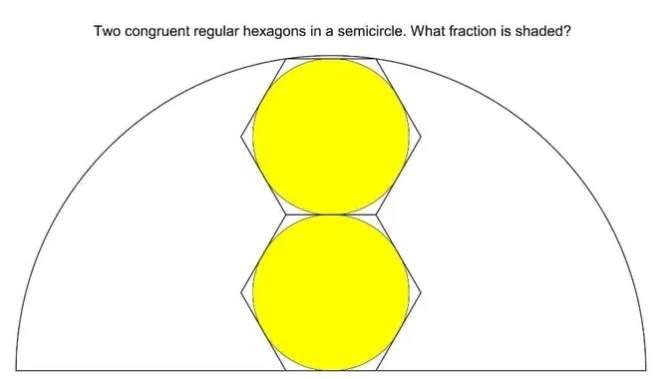
Mathematics Question and Solution
Let the side length of the two congruent inscribed regular hexagon be 1 unit each.
Calculating the radius, a, of one of the two congruent inscribed yellow circles.
tan60 = a/(0.5)
a = 0.8660254038 units.
a = ½√(3) units.
Therefore, area inscribed yellow circles is;
2πr²
= 2*π*(½√(3))²
= 2*π*¼*3
= ½(3π) square units.
Calculating the radius of the ascribed semi circle.
b² = 2-2cos120
b = √(3) units.
c = 2b
c = 2√(3) units.
d² = c²+0.5²
Where d is the radius of the ascribed semi circle.
It implies;
d² = (2√(3))²+0.5²
d² = 12+¼
d² = ¼(49)
d = √(49/4)
d = ½(7) units.
Again, d is the radius of the ascribed semi circle.
Area ascribed semi circle is;
½(πr²)
= ½*π*(7/2)*(7/2)
= = ⅛(49π) square units.
The shaded fraction is;
Area yellow inscribed circles ÷ Area ascribed semi circle.
= ½(3π)÷⅛(49π)
= 12/49