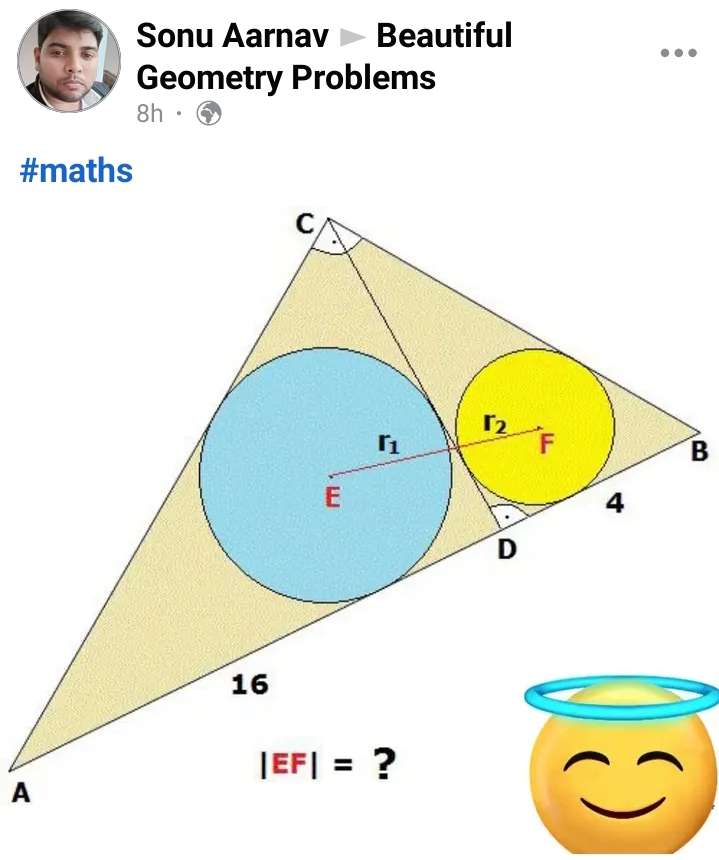
Mathematics Question and Solution
Considering similar triangles ADC and CDB ratios.
Let CD be a.
16 = a
a = 4
Cross Multiply.
a² = 64
a = 8 units
c² = 16²+8²
c = 8√(5) units.
c = AC.
Calculating r1.
16r1+8r1+8√(5)r1 = (16*8)
r1(24+8√(5)) = 128
r1 = 128/(24+8√(5))
r1 = 16/(3+√(5))
r1 = (12-4√(5)) units.
d² = 8²+4²
d = 4√(5) units.
d is BC.
Calculating r2.
4r2+8r2+4√(5)r2 = (8*4)
r2(12+4√(5)) = 32
r2(3+√(5)) = 8
r2 = 8/(3+√(5))
r2 = (6-2√(5)) units.
Calculating EF.
(EF)² = (r1+r2)²+(r1-r2)²
(EF)² = ((12-4√(5))+(6-2√(5)))²+((12-4√(5))-(6-2√(5)))²
(EF)² = (18-6√(5))²+(6-2√(5))²
EF = √(4.583592135²+1.527864045²)
EF = √(23.34368540004)
EF = 4.83153033728 units.