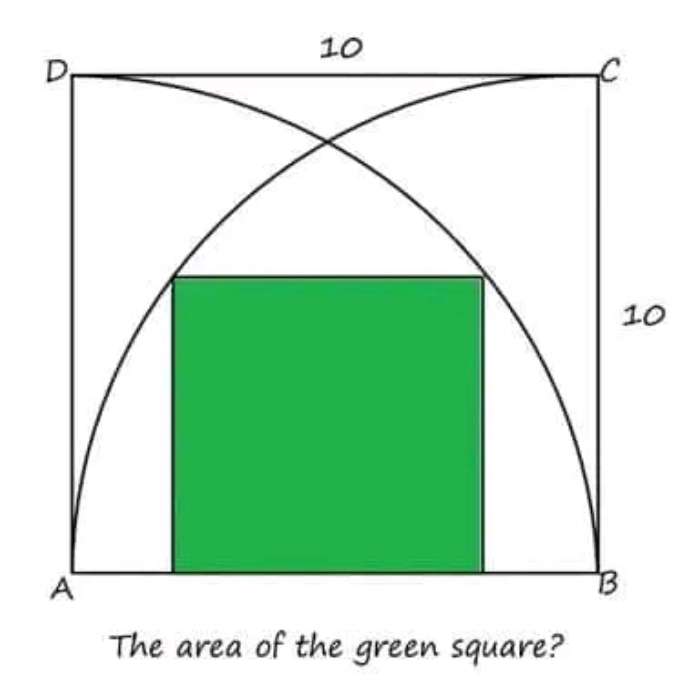
Mathematics Question and Solution
Let the side length of the inscribed green square be a.
b = ½(10-a) units.
c = b+a
c = ½(10-a+2a)
c = ½(10+a) units.
Therefore, a² (area green inscribed triangle) is;
10² = a²+(½(10+a))²
100 = a²+¼(100+20a+a²)
400 = 4a²+100+20a+a²
5a²+20a-300 = 0
a²+4a-60 = 0
Resolving the above quadratic equation via factorization approach to get a, side length of the inscribed green square.
a²+10a-6a-60 = 0
a(a+10)-6(a+10) = 0
(a+10)(a-6) = 0
It implies;
a ≠ -10
a = 6 units.
Therefore, area green inscribed square is;
a²
= 6²
= 36 square units.