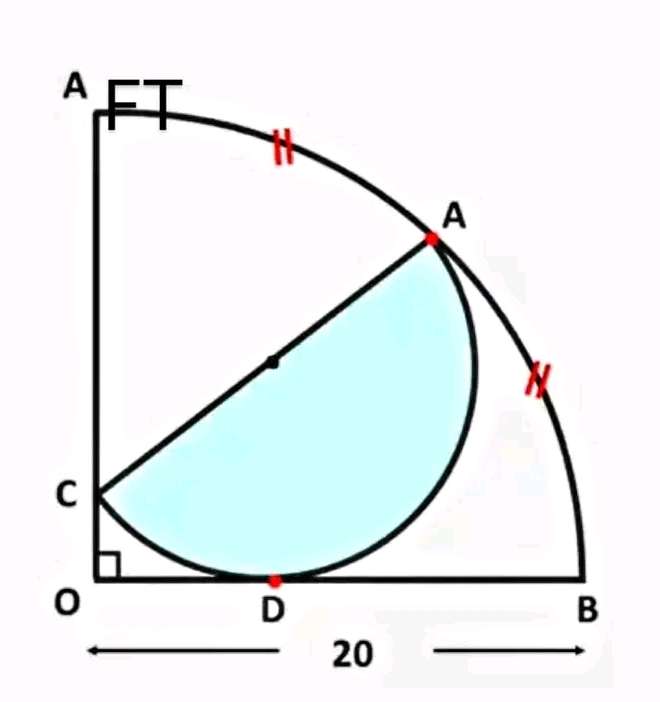
Mathematics Question and Solution
Let OC be a.
Let the radius of the inscribed blue half circle be b.
Calculating area inscribed blue half circle.
20² = 2c²
c = √(200)
c = 10√(2) units.
d = ½(c)
d = 5√(2) units.
d is OD.
Observing similar plane shape (right-angled) side length ratios to get a (OC).
a - 5√(2)
5√(2) - 10√(2)
Cross Multiply.
10√(2)a = 50
a = ½(5√(2)) units.
e = b-a
e = ½(2b-5√(2)) units.
It implies;
b² = (½(2b-5√(2)))²+(5√(2))²
b² = ¼(4b²-20√(2)b+50)+50
b² = b²-5√(2)b+(25/2)+50
10√(2)b = 125
2√(2)b = 25
b = ¼(25√(2)) units .
b = 6.25√(2) units.
b = 8.8388347648 units.
Again, b is the radius of the inscribed blue half circle.
Area inscribed blue half circle is;
0.5π*b²
= ½*π(¼(25√(2)))²
= (625π/16) square units.
= 122.7184630309 square units.